ЗжЮіЃКЃЈ1ЃЉИљОнЃКfЃЈxЃЉЁЪІИ
1ЧвfЃЈxЃЉ∉ІИ
2ЃЌПЩЕУy=
=x
2-2hx-hЃЌРћгУЖўДЮКЏЪ§ЕФЕЅЕїадПЩЕУ
-=hЁм0ЃЛгЩ
y==
x-2h-ЃЌyЁф=x+
ЃЌЖдhЗжРрЬжТлПЩЕУЃКЕБhЁн0ЃЌДЫЪБfЃЈxЃЉЁЪІИ
2ЃЛЕБhЃМ0ЪБЃЌ
yЁф=ЃЌКЏЪ§
дкxЁЪЃЈ0ЃЌ+ЁоЃЉгаМЋжЕЕуЃЌПЩЕУfЃЈxЃЉ∉ІИ
2ЃЎМДПЩЕУГіЃЎ
ЃЈ2ЃЉгЩfЃЈxЃЉЁЪІИ
1ЃЌШЁ0ЃМx
1ЃМx
2ЃМx
1+x
2ЃЌПЩЕУ
ЃМЃМЃЎгЩБэИёПЩжЊЃКfЃЈaЃЉ=dЃЌfЃЈbЃЉ=dЃЌfЃЈcЃЉ=tЃЌfЃЈa+b+cЃЉ=4ЃЌ0ЃМaЃМbЃМcЃМa+b+cЃЌРћгУЁАвЛНзБШдіКЏЪ§ЁБПЩЕУ
ЃМЃМЃМЃЌдйРћгУВЛЕШЪНЕФаджЪМДПЩЕУГіЃЎ
ЃЈ3ЃЉИљОнЁАЖўНзБШдіКЏЪ§ЁБЯШжЄУїfЃЈxЃЉЁм0ЖдxЁЪЃЈ0ЃЌ+ЁоЃЉГЩСЂЃЎдйжЄУїfЃЈxЃЉ=0дкЃЈ0ЃЌ+ЁоЃЉЩЯЮоНтЃЎМДПЩЕУГіЃЎ
НтД№ЃК
ЃЈ1ЃЉНтЃКy=
=x
2-2hx-hЃЌШєfЃЈxЃЉЁЪІИ
1ЃЌдђhЁм0ЃЛ
y==
x-2h-ЃЌyЁф=x+
ЃЌЕБhЁн0ЃЌxЃО0ЪБЃЌyЁфЃО0ЃЌДЫЪБfЃЈxЃЉЁЪІИ
2ЃЌВЛЗћКЯЬтвтЃЌЩсШЅЃЛ
ЕБhЃМ0ЪБЃЌ
yЁф=ЃЌДЫЪБКЏЪ§
дкxЁЪЃЈ0ЃЌ+ЁоЃЉгаМЋжЕЕуЃЌвђДЫfЃЈxЃЉ∉ІИ
2ЃЎ
злЩЯПЩЕУЃКЕБhЃМ0ЪБЃЌfЃЈxЃЉЁЪІИ
1ЧвfЃЈxЃЉ∉ІИ
2ЃЎ
вђДЫhЕФШЁжЕЗЖЮЇЪЧЃЈ-ЁоЃЌ0ЃЉЃЎ
ЃЈ2ЃЉжЄУїЃКгЩfЃЈxЃЉЁЪІИ
1ЃЌШєШЁ0ЃМx
1ЃМx
2ЃЌ
дђ
ЃМЃМЃЎ
гЩБэИёПЩжЊЃКfЃЈaЃЉ=dЃЌfЃЈbЃЉ=dЃЌfЃЈcЃЉ=tЃЌfЃЈa+b+cЃЉ=4ЃЌ
Ёп0ЃМaЃМbЃМcЃМa+b+cЃЌ
Ёр
ЃМЃМЃМЃЌ
ЁрdЃМ0ЃЌ
dЃМЃЌ
dЃМЃЌ
tЃМЃЌ
Ёр2d+tЃМ4ЃЌ
ЁрdЃЈ2d+t-4ЃЉЃО0ЃЎ
ЃЈЂѓЃЉЁпМЏКЯКЯІз={fЃЈxЃЉ|fЃЈxЃЉЁЪІИ
2ЃЌЧвДцдкГЃЪ§kЃЌЪЙЕУШЮШЁxЁЪЃЈ0ЃЌ+ЁоЃЉЃЌfЃЈxЃЉЃМk}ЃЌ
ЁрДцдкfЃЈxЃЉЁЪІзЃЌДцдкГЃЪ§kЃЌЪЙЕУ fЃЈxЃЉЃМk ЖдxЁЪЃЈ0ЃЌ+ЁоЃЉГЩСЂЃЎ
ЮвУЧЯШжЄУїfЃЈxЃЉЁм0ЖдxЁЪЃЈ0ЃЌ+ЁоЃЉГЩСЂЃЎ
МйЩшДцдкx
0ЁЪЃЈ0ЃЌ+ЁоЃЉЃЌЪЙЕУfЃЈx
0ЃЉЃО0ЃЌ
МЧ
=mЃО0
ЁпfЃЈxЃЉЪЧЖўНзБШдіКЏЪ§ЃЌМД
ЪЧдіКЏЪ§ЃЎ
ЁрЕБxЃОx
0ЪБЃЌ
ЃО
=mЃО0ЃЌ
ЁрfЃЈxЃЉЃОmx
2ЃЌ
ЁрвЛЖЈПЩвдевЕНвЛИіx
1ЃОx
0ЃЌЪЙЕУfЃЈx
1ЃЉЃОmx
12ЃОkЃЌ
етгыfЃЈxЃЉЃМk ЖдxЁЪЃЈ0ЃЌ+ЁоЃЉГЩСЂУЌЖмЃЎ
МДfЃЈxЃЉЁм0ЖдxЁЪЃЈ0ЃЌ+ЁоЃЉГЩСЂЃЎ
ЁрДцдкfЃЈxЃЉЁЪІзЃЌfЃЈxЃЉЁм0ЖдxЁЪЃЈ0ЃЌ+ЁоЃЉГЩСЂЃЎ
ЯТУцЮвУЧжЄУїfЃЈxЃЉ=0дкЃЈ0ЃЌ+ЁоЃЉЩЯЮоНтЃЎ
МйЩшДцдкx
2ЃО0ЃЌЪЙЕУfЃЈx
2ЃЉ=0ЃЌ
ЁпfЃЈxЃЉЪЧЖўНздіКЏЪ§ЃЌМД
ЪЧдіКЏЪ§ЃЎ
вЛЖЈДцдкx
3ЃОx
2ЃО0ЃЌЪЙ
ЃО
=0ЃЌетгыЩЯУцжЄУїЕФНсЙћУЌЖмЃЎ
ЁрfЃЈxЃЉ=0дкЃЈ0ЃЌ+ЁоЃЉЩЯЮоНтЃЎ
злЩЯЃЌЮвУЧЕУЕНДцдкfЃЈxЃЉЁЪІзЃЌfЃЈxЃЉЃМ0ЖдxЁЪЃЈ0ЃЌ+ЁоЃЉГЩСЂЃЎ
ЁрДцдкГЃЪ§MЁн0ЃЌЪЙЕУДцдкfЃЈxЃЉЁЪІзЃЌ?xЁЪЃЈ0ЃЌ+ЁоЃЉЃЌгаfЃЈxЃЉЃМMГЩСЂЃЎ
гжСюfЃЈxЃЉ=-
ЃЈxЃО0ЃЉЃЌдђfЃЈxЃЉЃМ0ЖдxЁЪЃЈ0ЃЌ+ЁоЃЉГЩСЂЃЌ
гжга
=-
дкЃЈ0ЃЌ+ЁоЃЉЩЯЪЧдіКЏЪ§ЃЌ
ЁрfЃЈxЃЉЁЪІзЃЌ
ЖјШЮШЁГЃЪ§kЃМ0ЃЌзмПЩвдевЕНвЛИіx
nЃО0ЃЌЪЙЕУxЃОx
nЪБЃЌгаfЃЈxЃЉЃОkЃЎ
ЁрMЕФзюаЁжЕ ЮЊ0ЃЎ



 УћЪІН№ЪжжИСьЯЮПЮЪБЯЕСаД№АИ
УћЪІН№ЪжжИСьЯЮПЮЪБЯЕСаД№АИ
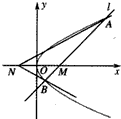 вбжЊЙ§ЕуMЃЈaЃЌ0ЃЉЃЈaЃО0ЃЉЕФЖЏжБЯпlНЛХзЮяЯпy2=4xгкAЁЂBСНЕуЃЌЕуNгыЕуMЙигкyжсЖдГЦЃЌ
вбжЊЙ§ЕуMЃЈaЃЌ0ЃЉЃЈaЃО0ЃЉЕФЖЏжБЯпlНЛХзЮяЯпy2=4xгкAЁЂBСНЕуЃЌЕуNгыЕуMЙигкyжсЖдГЦЃЌ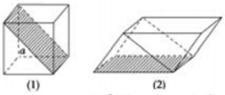 ШчЭМЃЈ1ЃЉЫљЪОЃЌвбжЊе§ЗНЬхУцЖдНЧЯпГЄЮЊaЃЌбивѕгАУцНЋЫќЧаИюГЩСНПщЃЌЦДГЩШчЭМЃЈ2ЃЉЫљЪОЕФМИКЮЬхЃЌФЧУДДЫМИКЮЬхЕФБэУцЛ§ЮЊЃЈЁЁЁЁЃЉ
ШчЭМЃЈ1ЃЉЫљЪОЃЌвбжЊе§ЗНЬхУцЖдНЧЯпГЄЮЊaЃЌбивѕгАУцНЋЫќЧаИюГЩСНПщЃЌЦДГЩШчЭМЃЈ2ЃЉЫљЪОЕФМИКЮЬхЃЌФЧУДДЫМИКЮЬхЕФБэУцЛ§ЮЊЃЈЁЁЁЁЃЉ