已知:有6个房间安排4个旅游者住,每人可以进住任一房间,且进住房间是等可能的,试求下列各事件的概率:
(1)事件A:指定的4个房间各有1人;
(2)事件B:恰有4个房间各有1人;
(3)事件C:指定的某个房间有2人.
【答案】
分析:(1)由题意知本题是一个古典概型每人可进住任1房间,进住哪间房是等可能的,每人都有6种等可能的方法,根据乘法原理,4人进住6个房间共有6
4种方法,而满足条件的指定的4个房间各有1人所以是4个人在4个位置的排列.
(2)由题意知本题是一个古典概型,每人可进住任1房间,进住哪间房是等可能的,每人都有6种等可能的方法,根据乘法原理,4人进住6个房间共有6
4种方法 而满足条件从6间中选出4间有C
64种方法,4个人每人去1间有A
44种方法.
(3)由题意知本题是一个古典概型每人可进住任1房间,根据乘法原理,4人进住6个房间共有6
4种方法,从4人中选2个人去指定的某个房间,余下2人每人都可去5个房间中的任1间,因而有5
2种种方法.
解答:解:(1)由题意知本题是一个古典概型
∵每人可进住任1房间,进住哪间房是等可能的,每人都有6种等可能的方法,
∴根据乘法原理,4人进住6个房间共有6
4种方法
而满足条件的指定的4个房间各有1人,有A
44种方法,
∴根据古典概型公式得到P=
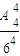
=
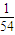
(2)由题意知本题是一个古典概型
∵每人可进住任1房间,进住哪间房是等可能的,每人都有6种等可能的方法,
∴根据乘法原理,4人进住6个房间共有6
4种方法
而满足条件从6间中选出4间有C
64种方法,
4个人每人去1间有A
44种方法
∴P=
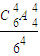
=
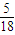
.
(3)由题意知本题是一个古典概型
∵每人可进住任1房间,进住哪间房是等可能的,每人都有6种等可能的方法,
∴根据乘法原理,4人进住6个房间共有6
4种方法
从4人中选2个人去指定的某个房间,共有C
42种选法,余下2人每人都可去5个房间中的任1间,因而有5
2种种方法.
∴P=
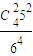
=
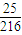
.
点评:本题主要考查排列组合,排列、排列数公式及解排列的应用题,它研究的对象以及研究问题的方法都和前面掌握的知识不同,内容抽象,解题方法比较灵活.

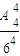 =
=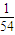
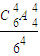 =
=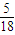 .
.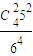 =
=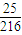 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案