
【题目】如图,太湖一个角形湖湾![]() ( 常数
( 常数![]() 为锐角). 拟用长度为
为锐角). 拟用长度为![]() (
(![]() 为常数)的围网围成一个养殖区,有以下两种方案可供选择:
为常数)的围网围成一个养殖区,有以下两种方案可供选择:
方案一 如图1,围成扇形养殖区![]() ,其中
,其中![]() ;
;
方案二 如图2,围成三角形养殖区![]() ,其中
,其中![]() ;
;
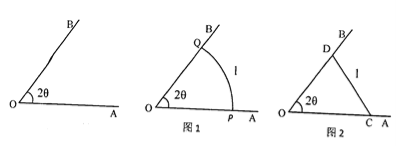
(1)求方案一中养殖区的面积![]() ;
;
(2)求方案二中养殖区的最大面积![]() ;
;
(3)为使养殖区的面积最大,应选择何种方案?并说明理由.
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】观察下列方程,并回答问题:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;…
;…
(1)请你根据这列方程的特点写出第![]() 个方程;
个方程;
(2)直接写出第2009个方程的根;
(3)说出这列方程的根的一个共同特点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,上顶点为
,上顶点为![]() ,过
,过![]() 与
与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于
轴负半轴于![]() 点,且
点,且![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若过![]() 、
、![]() 、
、![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() 相切,求椭圆
相切,求椭圆![]() 的方程;
的方程;
(3)过![]() 的直线
的直线![]() 与(2)中椭圆交于不同的两点
与(2)中椭圆交于不同的两点![]() 、
、![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() 经过点A (1,0).
经过点A (1,0).
(1)若直线![]() 与圆C相切,求直线
与圆C相切,求直线![]() 的方程;
的方程;
(2)若直线![]() 与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线
与圆C相交于P,Q两点,求三角形CPQ面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
B. 在线性回归分析中,回归直线不一定过样本点的中心![]()
C. 在回归分析中, ![]() 为0.98的模型比
为0.98的模型比![]() 为0.80的模型拟合的效果好
为0.80的模型拟合的效果好
D. 自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一项针对人们休闲方式的调查结果如下:受调查对象总计124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 的列联表;
的列联表;
(2)根据下列提供的独立检验临界值表,你最多能有多少把握认为性别与休闲方式有关系?
独立检验临界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
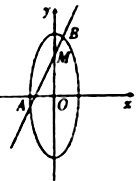
【题目】如图,已知焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的中心是原点
的中心是原点![]() ,离心率为
,离心率为![]() ,以椭圆
,以椭圆![]() 的端州的两端点和两焦点所围成的四边形的周长为8,直线
的端州的两端点和两焦点所围成的四边形的周长为8,直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com