
分析 利用多项式乘多项式把($\overrightarrow{a}$+2$\overrightarrow{b}$)($\overrightarrow{a}$-3$\overrightarrow{b}$)=-72的左边展开,再把$\overrightarrow{a}$与$\overrightarrow{b}$夹角为$\frac{π}{3}$,|$\overrightarrow{b}$|=4代入化为关于$|\overrightarrow{a}|$的一元二次方程,则答案可求.
解答 解:由($\overrightarrow{a}$+2$\overrightarrow{b}$)($\overrightarrow{a}$-3$\overrightarrow{b}$)=-72,得$|\overrightarrow{a}{|}^{2}-\overrightarrow{a}•\overrightarrow{b}-6|\overrightarrow{b}{|}^{2}=-72$,
即$|\overrightarrow{a}{|}^{2}-|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>-6|\overrightarrow{b}{|}^{2}=-72$,
又$\overrightarrow{a}$与$\overrightarrow{b}$夹角为$\frac{π}{3}$,|$\overrightarrow{b}$|=4,
∴$|\overrightarrow{a}{|}^{2}-2|\overrightarrow{a}|-24=0$,解得|$\overrightarrow{a}$|=6.
故答案为:6.
点评 本题考查平面向量的数量积运算,关键是对数量积公式的记忆,是中档题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源: 题型:解答题
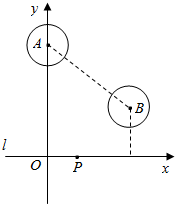 如图l是东西走向的一水管,在水管北侧有两个半径都是10m的圆形蓄水池A,B(A,B分别为蓄水池的圆心),经测量,点A,B到水管l的距离分别为55m和25m,AB=50m.以l所在直线为x轴,过点A且与l垂直的直线为y轴,建立如图所示的直角坐标系(O为坐标原点).
如图l是东西走向的一水管,在水管北侧有两个半径都是10m的圆形蓄水池A,B(A,B分别为蓄水池的圆心),经测量,点A,B到水管l的距离分别为55m和25m,AB=50m.以l所在直线为x轴,过点A且与l垂直的直线为y轴,建立如图所示的直角坐标系(O为坐标原点).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | -$\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a?α,b?α,且a∥β,b∥β,则α∥β | |
| B. | a、b是异面直线,则存在唯一的平面与a、b等距 | |
| C. | a⊥α,b?β,a⊥b,则α∥β | |
| D. | α⊥γ,γ∥β,a⊥α,b⊥β,则a⊥b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0.875 | C. | 0.65 | D. | 0.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com