
设函数 。
。
(Ⅰ)若 时,函数
时,函数 取得极值,求函数
取得极值,求函数 的图像在
的图像在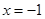 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在区间
在区间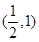 内不单调,求实数
内不单调,求实数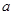 的取值范围。
的取值范围。
(Ⅰ)切线方程为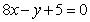 ;(Ⅱ)
;(Ⅱ)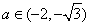 .
.
解析试题分析:(Ⅰ)求函数 的图像在
的图像在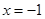 处的切线方程,首先求出函数
处的切线方程,首先求出函数 的解析式,而已知若
的解析式,而已知若 时,函数
时,函数 取得极值,因此先求出数
取得极值,因此先求出数 的导函数,令导函数在
的导函数,令导函数在 处的值为
处的值为 ,求出
,求出 的解析式,将
的解析式,将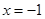 代入
代入 求出切点坐标,将
求出切点坐标,将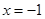 代入导函数求出切线的斜率,利用点斜式求出切线的方程.(Ⅱ)若函数
代入导函数求出切线的斜率,利用点斜式求出切线的方程.(Ⅱ)若函数 在区间
在区间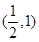 内不单调,即函数
内不单调,即函数 在区间
在区间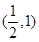 有极值,即导函数
有极值,即导函数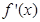 在区间
在区间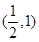 上有解,令导函数
上有解,令导函数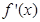 为
为 ,分离出
,分离出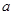 得
得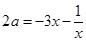 ,求出
,求出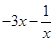 在
在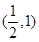 上的范围,从而得实数
上的范围,从而得实数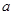 的取值范围.
的取值范围.
试题解析:(Ⅰ)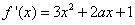 由
由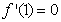 得
得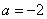
∴ 当
当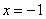 时,
时,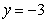 即切点
即切点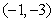
 令
令 得
得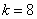 ∴切线方程为
∴切线方程为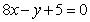 ;
;
(Ⅱ) 在区间
在区间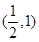 内不单调,即
内不单调,即 在
在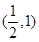 有解,所以
有解,所以 ,
,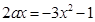 ,由
,由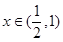 ,
,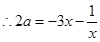 ,令
,令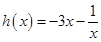 ,
,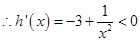 ,知
,知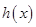 在
在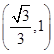 单调递减,在
单调递减,在 ,所以
,所以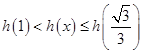 ,即
,即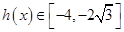 ,
,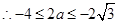 ,即
,即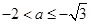 ,而当
,而当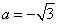 时,
时,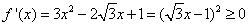 ∴舍去 综上
∴舍去 综上 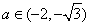
考点:函数在某点取得极值的条件;函数的单调性与导数的关系;利用导数研究曲线上某点切线方程.


科目:高中数学 来源: 题型:解答题
已知函数
 ,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
⑴求函数 的解析式;
的解析式;
⑵若对于区间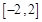 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ,求实数
,求实数 的最小值;
的最小值;
⑶若过点
 ,可作曲线
,可作曲线 的三条切线,求实数
的三条切线,求实数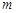 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数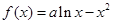 .
.
(1)当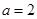 时,求函数
时,求函数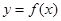 在
在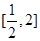 上的最大值;
上的最大值;
(2)令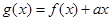 ,若
,若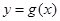 在区间
在区间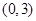 上不单调,求
上不单调,求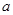 的取值范围;
的取值范围;
(3)当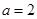 时,函数
时,函数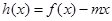 的图象与
的图象与 轴交于两点
轴交于两点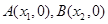 ,且
,且 ,又
,又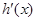 是
是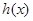 的导函数.若正常数
的导函数.若正常数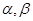 满足条件
满足条件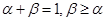 .证明:
.证明: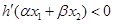 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数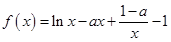 .
.
(1)当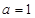 时,求曲线
时,求曲线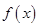 在
在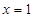 处的切线方程;
处的切线方程;
(2)当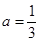 时,求函数
时,求函数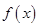 的单调区间;
的单调区间;
(3)在(2)的条件下,设函数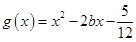 ,若对于
,若对于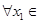 [1,2],
[1,2],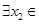 [0,1],使
[0,1],使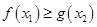 成立,求实数
成立,求实数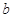 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地区注重生态环境建设,每年用于改造生态环境总费用为 亿元,其中用于风景区改造为
亿元,其中用于风景区改造为 亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用
亿元。该市决定建立生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用 随每年改造生态环境总费用
随每年改造生态环境总费用 增加而增加;②每年改造生态环境总费用至少
增加而增加;②每年改造生态环境总费用至少 亿元,至多
亿元,至多 亿元;③每年用于风景区改造费用
亿元;③每年用于风景区改造费用 不得低于每年改造生态环境总费用
不得低于每年改造生态环境总费用 的15%,但不得高于每年改造生态环境总费用
的15%,但不得高于每年改造生态环境总费用 的25%.
的25%.
若 ,
, ,请你分析能否采用函数模型y=
,请你分析能否采用函数模型y=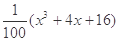 作为生态环境改造投资方案.
作为生态环境改造投资方案.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数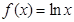 ,
,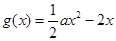 .
.
(Ⅰ)若曲线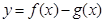 在
在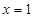 与
与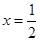 处的切线相互平行,求
处的切线相互平行,求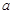 的值及切线斜率;
的值及切线斜率;
(Ⅱ)若函数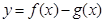 在区间
在区间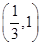 上单调递减,求
上单调递减,求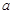 的取值范围;
的取值范围;
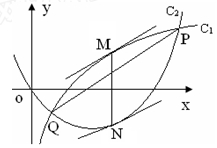
(Ⅲ)设函数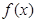 的图像C1与函数
的图像C1与函数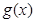 的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.
的图像C2交于P、Q两点,过线段PQ的中点作x轴的垂线分别交C1、C2于点M、N,证明:C1在点M处的切线与C2在点N处的切线不可能平行.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,函数
,函数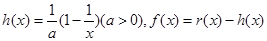 .
.
(I)试求f(x)的单调区间。
(II)若f(x)在区间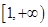 上是单调递增函数,试求实数a的取值范围:
上是单调递增函数,试求实数a的取值范围:
(III)设数列 是公差为1.首项为l的等差数列,数列
是公差为1.首项为l的等差数列,数列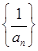 的前n项和为
的前n项和为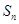 ,求证:当
,求证:当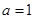 时,
时,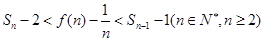 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数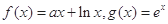 .
.
(I)当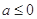 时,求
时,求 的单调区间
的单调区间
(Ⅱ)若不等式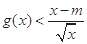 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;
(Ⅲ)定义:对于函数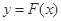 和
和 在其公共定义域内的任意实数
在其公共定义域内的任意实数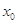 ,称
,称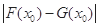 的值为两函数在
的值为两函数在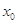 处的差值。证明:当
处的差值。证明:当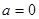 时,函数
时,函数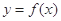 和
和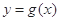 在其公共定义域内的所有差值都大干2。
在其公共定义域内的所有差值都大干2。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com