
【题目】定义域为R的奇函数f(x)= ![]() ,其中h(x)是指数函数,且h(2)=4.
,其中h(x)是指数函数,且h(2)=4.
(1)求函数f(x)的解析式;
(2)求不等式f(2x﹣1)>f(x+1)的解集.
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点. 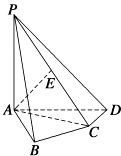
(1)求PB和平面PAD所成的角的大小;
(2)证明:AE⊥平面PCD;
(3)求二面角A﹣PD﹣C得到正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:
物体重量(单位g) | 1 | 2 | 3 | 4 | 5 |
弹簧长度(单位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
参考公式:
①.样本数据x1 , x2 , …xn的标准差
s= ![]() ,其中
,其中 ![]() 为样本的平均数;
为样本的平均数;
②.线性回归方程系数公式 ![]() =
= 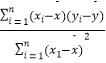 =
= 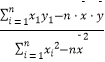 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.
(1)画出散点图;
(2)利用所给的参考公式,求y对x的回归直线方程;
(3)预测所挂物体重量为8g时的弹簧长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知点A(1,0),D(﹣1,0),点B,C在单位圆O上,且∠BOC= ![]() .
. 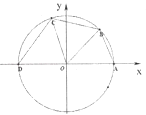
(Ⅰ)若点B( ![]() ,
, ![]() ),求cos∠AOC的值;
),求cos∠AOC的值;
(Ⅱ)设∠AOB=x(0<x< ![]() ),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
),四边形ABCD的周长为y,将y表示成x的函数,并求出y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.
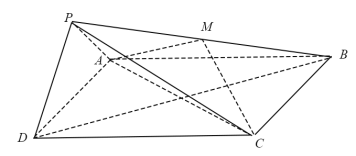
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中 ①若loga3>logb3,则a>b;
②函数f(x)=x2﹣2x+3,x∈[0,+∞)的值域为[2,+∞);
③设g(x)是定义在区间[a,b]上的连续函数.若g(a)=g(b)>0,则函数g(x)无零点;
④函数 ![]() 既是奇函数又是减函数.
既是奇函数又是减函数.
其中正确的命题有
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2bx+c,且f(1)=f(3)=﹣1.设a>0,将函数f(x)的图像先向右平移a个单位长度,再向下平移a2个单位长度,得到函数g(x)的图像. (Ⅰ)若函数g(x)有两个零点x1 , x2 , 且x1<4<x2 , 求实数a的取值范围;
(Ⅱ)设连续函数在区间[m,n]上的值域为[λ,μ],若有 ![]() ,则称该函数为“陡峭函数”.若函数g(x)在区间[a,2a]上为“陡峭函数”,求实数a的取值范围.
,则称该函数为“陡峭函数”.若函数g(x)在区间[a,2a]上为“陡峭函数”,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知递增等比数列{an}的第三项、第五项、第七项的积为512,且这三项 分别减去1,3,9后成等差数列.
(1)求{an}的首项和公比;
(2)设Sn=a12+a22+…+an2 , 求Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com