Question

2．函数f（x）=$\sqrt{{x}^{2}+1}$+$\sqrt{{x}^{2}-6x+25}$取最小值时，x为$\frac{3}{5}$．

Answer 1

分析 函数f（x）=$\sqrt{{x}^{2}+1}$+$\sqrt{{x}^{2}-6x+25}$，即求x轴上点（x，0）到两定点（3，4），（0，-1）距离和的最小值，而两点位于x轴的两侧，所以最小值即两点的距离，再由三点共线，斜率相等，即可得到所求值．

解答 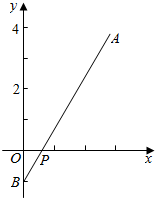解：函数f（x）=$\sqrt{{x}^{2}+1}$+$\sqrt{{x}^{2}-6x+25}$
=$\sqrt{（x-0）^{2}+[0-（-1）]^{2}}$+$\sqrt{（x-3）^{2}+（0-4）^{2}}$
表示x轴上点P（x，0）到两定点A（3，4），B（0，-1）距离和，
而两点位于x轴的两侧，所以最小值即两点A，B的距离
$\sqrt{（3-0）^{2}+（4+1）^{2}}$=$\sqrt{34}$．
此时由k_AB=k_PB，即$\frac{4+1}{3-0}$=$\frac{0+1}{x-0}$，可得x=$\frac{3}{5}$．
故答案为：$\frac{3}{5}$．

点评 本题考查求函数的最小值，注意运用几何意义，借助两点的距离最小，考查学生分析解决问题的能力，正确转化是关键．