
【题目】某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响.已知某学生选修甲而不选修乙和丙的概率为0.08,选修甲和乙而不选修丙的概率是0.12,至少选修一门的概率是0.88,用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积.
(1)记“函数f(x)=x2+ξx为R上的偶函数”为事件A,求事件A的概率;
(2)求ξ的分布列和数学期望.
【答案】
(1)解:设该学生选修甲、乙、丙的概率分别为x、y、z
依题意得 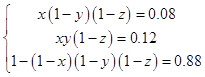 ,解得
,解得 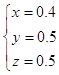
若函数f(x)=x2+ξx为R上的偶函数,则ξ=0
当ξ=0时,表示该学生选修三门功课或三门功课都没选.
∴P(A)=P(ξ=0)=xyz+(1﹣x)(1﹣y)(1﹣z)
=0.4×0.5×0.6+(1﹣0.4)(1﹣0.5)(1﹣0.6)=0.24
∴事件A的概率为0.24
(2)解:依题意知ξ的取值为0和2由(1)所求可知
P(ξ=0)=0.24
P(ξ=2)=1﹣P(ξ=0)=0.76
则ξ的分布列为
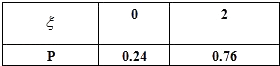
∴ξ的数学期望为Eξ=0×0.24+2×0.76=1.52
【解析】(1)由于学生是否选修哪门课互不影响,利用相互独立事件同时发生的概率解出学生选修甲、乙、丙的概率,由题意得到ξ=0时,表示该学生选修三门功课或三门功课都没选,根据互斥事件的概率公式得到结果.(2)用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积,所以变量的取值是0或2,结合第一问解出概率,写出分布列,算出期望.
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元.
(Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,n∈N)的函数解析式f(n);
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得表:
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个小组各10名学生的英语口语测试成绩如下(单位:分).
甲组:76,90,84,86,81,87,86,82,85,83 乙组:82,84,85,89,79,80,91,89,79,74
现从这20名学生中随机抽取一人,将“抽出的学生为甲组学生”记为事件A;“抽出学生的英语口语测试成绩不低于85分”记为事件B,则P(AB)、P(A|B)的值分别是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}满足an=2an﹣1+2n+1(n∈N* , n≥2),a3=27.
(1)求a1 , a2的值;
(2)是否存在一个实数t,使得bn= ![]() (an+t)(n∈N*),且数列{bn}为等差数列?若存在,求出实数t;若不存在,请说明理由;
(an+t)(n∈N*),且数列{bn}为等差数列?若存在,求出实数t;若不存在,请说明理由;
(3)求数列{an}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1底面是边长为1的正方形,高AA1= ![]() ,点A是平面α内的一个定点,AA1与α所成角为
,点A是平面α内的一个定点,AA1与α所成角为 ![]() ,点C1在平面α内的射影为P,当四棱柱ABCD﹣A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积= .
,点C1在平面α内的射影为P,当四棱柱ABCD﹣A1B1C1D1按要求运动时(允许四棱柱上的点在平面α的同侧或异侧),点P所经过的区域的面积= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,从该地区调查了500位老人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿提供帮助的老年人的比例;
(2)能否有99℅的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?提供帮助的老年人的比例?说明理由.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
附:
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com