
分析 (1)根据f(1)=0,可得a,b,c的关系,再根据3a>2c>2b,将其中的c代换成a与b表示,即可证明:a>0且b<0;
(2)求出f(2)的值,根据已知条件,分别对c的正负情况进行讨论即可;
(3)根据韦达定理,将|x1-x2|转化成用两个根表示,然后转化成用$\frac{b}{a}$表示,运用(1)的结论,即可求得|x1-x2|的取值范围.
解答 解:(1)∵f(1)=a+b+c=-$\frac{a}{2}$,
∴3a+2b+2c=0.
又3a>2c>2b.
(2)根据题意有f(0)=0,f(2)=4a+2b+c=(3a+2b+2c)+a-c=a-c.
下面对c的正负情况进行讨论:
①当c>0时,∵a>0,
∴f(0)=c>0,f(1)=-$\frac{a}{2}$<0
∴函数f(x)在区间(0,1)内至少有一个零点;
②当c≤0时,∵a>0,
∴f(1)=-$\frac{a}{2}$<0,f(2)=a-c>0
∴函数f(x)在区间(1,2)内至少有一个零点;
综合①②得函数f(x)在区间(0,2)内至少有一个零点;
(3)∵x1,x2是函数f(x)的两个零点
∴x1,x2是方程ax2+bx+c=0的两根.
故x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$=$\frac{-\frac{3a+2b}{2}}{a}$=$-\frac{3}{2}-\frac{b}{a}$
从而|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{({-\frac{b}{a})}^{2}-4(-\frac{3}{2}-\frac{b}{a})}$=$\sqrt{({\frac{b}{a}+2)}^{2}+2}$.
∵由(1)知a>0,b<0,
又2c=-3a-2b及3a>2c>2b知3a>-3a-2b>2b
∵a>0,∴3>-3-$\frac{2b}{a}$>2•$\frac{b}{a}$,
即-3<$\frac{b}{a}$<-$\frac{3}{4}$,
∴$\sqrt{2}≤$|x1-x2|$<\frac{\sqrt{57}}{4}$.
点评 本题考查了二次函数的性质,对于二次函数要注意数形结合的应用,注意抓住二次函数的开口方向,对称轴,以及判别式的考虑;难度较大.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
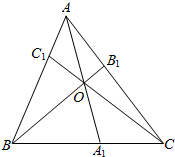 如图,已知点O是△ABC内任意一点,连结AO,BO,CO,并延长交对边于A1,B1,C1,则$\frac{{O{A_1}}}{{A{A_1}}}+\frac{{O{B_1}}}{{B{B_1}}}+\frac{{O{C_1}}}{{C{C_1}}}=1$,类比猜想:点O是空间四面体V-BCD内的任意一点,连结VO,BO,CO,DO并延长分别交面BCD,VCD,VBD,VBC于点V1,B1,C1,D1,则有$\frac{{O{V_1}}}{{V{V_1}}}+\frac{{O{B_1}}}{{B{B_1}}}+\frac{{O{C_1}}}{{C{C_1}}}+\frac{{O{D_1}}}{{D{D_1}}}=1$.
如图,已知点O是△ABC内任意一点,连结AO,BO,CO,并延长交对边于A1,B1,C1,则$\frac{{O{A_1}}}{{A{A_1}}}+\frac{{O{B_1}}}{{B{B_1}}}+\frac{{O{C_1}}}{{C{C_1}}}=1$,类比猜想:点O是空间四面体V-BCD内的任意一点,连结VO,BO,CO,DO并延长分别交面BCD,VCD,VBD,VBC于点V1,B1,C1,D1,则有$\frac{{O{V_1}}}{{V{V_1}}}+\frac{{O{B_1}}}{{B{B_1}}}+\frac{{O{C_1}}}{{C{C_1}}}+\frac{{O{D_1}}}{{D{D_1}}}=1$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 一质点的移动方式,如图所示,在第1分钟,它从原点移动到点(1,0),接下来它便依图上所示的方向,在x,y轴的正向前进或后退,每1分钟只走1单位且平行其中一轴,则2016分钟结束之时,质点的位置坐标是(44,8).
一质点的移动方式,如图所示,在第1分钟,它从原点移动到点(1,0),接下来它便依图上所示的方向,在x,y轴的正向前进或后退,每1分钟只走1单位且平行其中一轴,则2016分钟结束之时,质点的位置坐标是(44,8).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 1 | C. | π | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com