
| A. | $\frac{1}{63}$ | B. | $\frac{1}{31}$ | C. | $\frac{3}{61}$ | D. | $\frac{1}{15}$ |
分析 观察数列的特征,得出它的项数是1+2+3+…+k=$\frac{k(k+1)}{2}$(k∈N*),在每一个k段内是k个分数(k∈N*,k≥3),且它们的分子分母和为k+1;进而求出第2016项即可.
解答 解:观察数列:$\frac{1}{1}$,$\frac{2}{1}$,$\frac{1}{2}$,$\frac{3}{1}$,$\frac{2}{2}$,$\frac{1}{3}$,$\frac{4}{1}$,$\frac{3}{2}$,$\frac{2}{3}$,$\frac{1}{4}$,…,得出:
它的项数是1+2+3+…+k=$\frac{k(k+1)}{2}$(k∈N*),
并且在每一个k段内,是$\frac{k}{1}$,$\frac{k-1}{2}$,$\frac{k-2}{3}$,…,$\frac{2}{k-2}$,$\frac{1}{k-1}$,$\frac{1}{k}$(k∈N*,k≥3);
令$\frac{k(k+1)}{2}$≥2016(k∈N*),
得$\frac{63×64}{2}$=2016;
又第n组是由分子、分母之和为n+1知:
2016项位于倒数第1个数,
∴该数列的第2016项为a2016=$\frac{1}{63}$.
故选:A.
点评 本题考查了数列的应用问题,解题时应根据数列的特征,总结出规律,才能得出正确的结论.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
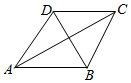 如图所示,四边形ABCD中,AB=AD=2,△BCD为正三角形,设∠BAD=α(α∈(0,π)).
如图所示,四边形ABCD中,AB=AD=2,△BCD为正三角形,设∠BAD=α(α∈(0,π)).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有两个面平行,其余各面都是四边形,并且每相邻的两个四边形的公共边都互相平行的几何体叫棱柱 | |
| B. | 圆锥的过轴的截面是一个等腰三角形 | |
| C. | 直角三角形绕它的一条边旋转一周形成的曲面围成的几何体是圆锥 | |
| D. | 圆台平行于底面的截面是圆面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com