Question

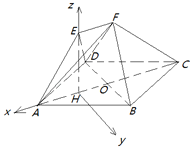
【题目】如图，多面体EF﹣ABCD中，四边形ABCD是菱形，AB=4，∠BAD=60°，AC，BD相交于O，EF∥AC，点E在平面ABCD上的射影恰好是线段AO的中点．

（Ⅰ）求证：BD⊥平面ACF；

（Ⅱ）若直线AE与平面ABCD所成的角为45°，求平面DEF与平面ABCD所成角（锐角）的余弦值．

Answer 1

【答案】（1）见解析（2）

【解析】分析：（Ⅰ）取AO的中点H，连结EH，证明EH⊥BD，AC⊥BD，即BD⊥平面ACF

（Ⅱ）由（Ⅰ）知EH⊥平面ABCD，以H为原点，如图所示建立空间直角坐标系H﹣xyz，

由EH⊥平面ABCD，得∠EAH为AE与平面ABCD所成的角，即∠EAH=45°则

求出平面DEF与平面ABCD的法向量，代入公式即可求解．

详解：（Ⅰ）取AO的中点H，连结EH，则EH⊥平面ABCD

∵BD在平面ABCD内，∴EH⊥BD

又菱形ABCD中，AC⊥BD 且EH∩AC=H，EH、AC在平面EACF内

∴BD⊥平面EACF，即BD⊥平面ACF

（Ⅱ）由（Ⅰ）知EH⊥平面ABCD，以H为原点，如图所示建立空间直角坐标系H﹣xyz

∵EH⊥平面ABCD，∴∠EAH为AE与平面ABCD所成的角，

即∠EAH=45°，又菱形ABCD的边长为4，则

各点坐标分别为，

E（0，0，）

易知为平面ABCD的一个法向量，记=，=，=

∵EF∥AC，∴=

设平面DEF的一个法向量为（注意：此处可以用替代）

即 =，

令，则，∴

∴

平面DEF与平面ABCD所成角（锐角）的余弦值为．