Question

19．已知抛物线C：x²=2y的焦点为F，P为抛物线C上任意一点，点M（-2，4^m-2^m+4），m∈R，则|MP|+|PF|的最小值为（　　）

• A． $\frac{5}{2}$
• B． $\frac{13}{4}$
• C． $\frac{9}{2}$
• D． $\frac{17}{4}$

Answer 1

分析 求出抛物线的焦点和准线方程，判断M在抛物线的开口之内，过M作准线的垂线，交于N，当M．P，N共线时，|PM|+|PF|取得最小值，即为|MN|，再由配方结合二次函数的最值的求法，即可得到最小值．

解答 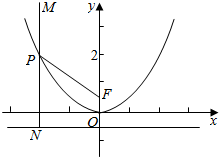解：抛物线C：x²=2y的焦点为F（0，$\frac{1}{2}$），
准线方程为y=-$\frac{1}{2}$，
4^m-2^m+4=（2^m-$\frac{1}{2}$）²+$\frac{15}{4}$＞2，
可得M在抛物线的开口之内，
过M作准线的垂线，交于N，
由抛物线的定义可得，|PM|+|PF|≥|MP|+|PN|，
当M．P，N共线时，|PM|+|PF|取得最小值，
即为|MN|=4^m-2^m+4+$\frac{1}{2}$=（2^m-$\frac{1}{2}$）²+$\frac{17}{4}$，
当m=-1时，取得最小值为$\frac{17}{4}$．
故选D．

点评 本题考查抛物线的定义、方程的运用，考查最值的求法，注意运用定义法，结合两点之间线段最短，考查运算能力，属于中档题．