【答案】
分析:(1)化简函数y=2sin
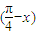
为y=-2sin
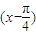
.利用y=sinu(u∈R)的递增、递减区间,求出函数y=2sin
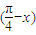
的单调递减区间、单调递增区间.
(2)直接利用正切函数的周期公式求法,求y=3tan

的周期,结合y=3tan
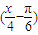
的单调增区间,求出y=3tan
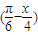
的单调递减区间.即可.
解答:解:(1)y=2sin

化成y=-2sin
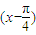
.
∵y=sinu(u∈R)的递增、递减区间分别为

(k∈Z),

(k∈Z),
∴函数y=-2sin
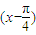
的递增、递减区间分别由下面的不等式确定
2kπ+
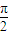
≤x-
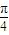
≤2kπ+
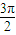
(k∈Z),即2kπ+
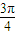
≤x≤2kπ+

(k∈Z),
2kπ-
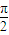
≤x-
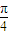
≤2kπ+
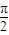
(k∈Z),即2kπ-
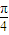
≤x≤2kπ+

(k∈Z).
∴函数y=2sin
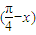
的单调递减区间、单调递增区间分别为

(k∈Z),
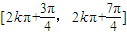
(k∈Z).
(2)求y=3tan

的周期及单调区间.y=3tan

=-3tan
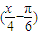
,
∴T=
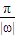
=4π,∴y=3tan
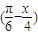
的周期为4π.由kπ-

<
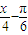
<kπ+

,
得4kπ-
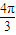
<x<4kπ+
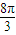
(k∈Z),y=3tan
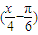
的单调增区间是

(k∈Z)∴y=3tan
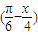
的单调递减区间是
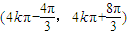 点评:
点评:本题考查正切函数的单调性,三角函数的周期性及其求法,正弦函数的单调性,在求函数y=2sin
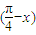
的单调区间时,必须把函数化为y=-2sin
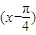
,否则结果一定有错误,这是一个常考点,易错点.本题是基础题.

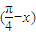 的单调区间.
的单调区间.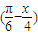 的周期及单调区间.
的周期及单调区间.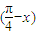 为y=-2sin
为y=-2sin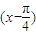 .利用y=sinu(u∈R)的递增、递减区间,求出函数y=2sin
.利用y=sinu(u∈R)的递增、递减区间,求出函数y=2sin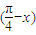 的单调递减区间、单调递增区间.
的单调递减区间、单调递增区间. 的周期,结合y=3tan
的周期,结合y=3tan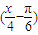 的单调增区间,求出y=3tan
的单调增区间,求出y=3tan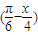 的单调递减区间.即可.
的单调递减区间.即可. 化成y=-2sin
化成y=-2sin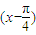 .
. (k∈Z),
(k∈Z), (k∈Z),
(k∈Z),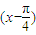 的递增、递减区间分别由下面的不等式确定
的递增、递减区间分别由下面的不等式确定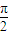 ≤x-
≤x-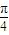 ≤2kπ+
≤2kπ+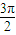 (k∈Z),即2kπ+
(k∈Z),即2kπ+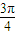 ≤x≤2kπ+
≤x≤2kπ+ (k∈Z),
(k∈Z),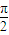 ≤x-
≤x-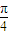 ≤2kπ+
≤2kπ+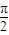 (k∈Z),即2kπ-
(k∈Z),即2kπ-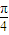 ≤x≤2kπ+
≤x≤2kπ+ (k∈Z).
(k∈Z).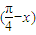 的单调递减区间、单调递增区间分别为
的单调递减区间、单调递增区间分别为 (k∈Z),
(k∈Z),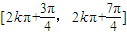 (k∈Z).
(k∈Z). 的周期及单调区间.y=3tan
的周期及单调区间.y=3tan =-3tan
=-3tan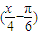 ,
,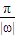 =4π,∴y=3tan
=4π,∴y=3tan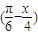 的周期为4π.由kπ-
的周期为4π.由kπ- <
<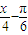 <kπ+
<kπ+ ,
,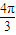 <x<4kπ+
<x<4kπ+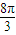 (k∈Z),y=3tan
(k∈Z),y=3tan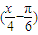 的单调增区间是
的单调增区间是 (k∈Z)∴y=3tan
(k∈Z)∴y=3tan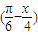 的单调递减区间是
的单调递减区间是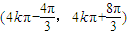
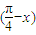 的单调区间时,必须把函数化为y=-2sin
的单调区间时,必须把函数化为y=-2sin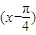 ,否则结果一定有错误,这是一个常考点,易错点.本题是基础题.
,否则结果一定有错误,这是一个常考点,易错点.本题是基础题. 
