
| A. | y=x+$\frac{4}{x}$ | B. | y=sinx+$\frac{4}{sinx}$ | ||
| C. | y=21+x+21-x | D. | y=x2+$\frac{1}{{x}^{2}+1}$+3,x≠0 |
分析 由基本不等式求最值的规律,逐个选项验证可得.
解答 解:选项A,若x<0则x+$\frac{4}{x}$≤-2$\sqrt{x•\frac{4}{x}}$=-4,不满足最小值是4,故错误;
选项B,由基本不等式可得当且仅当sinx=$\frac{4}{sinx}$即sinx=±2取等号,由三角函数可知不成立,故错误;
选项C,y=21+x+21-x≥2$\sqrt{{2}^{1+x}•{2}^{1-x}}$=4,当且仅当21+x=21-x即x=0时取等号,故正确;
选项D,y=x2+$\frac{1}{{x}^{2}+1}$+3=x2+1+$\frac{1}{{x}^{2}+1}$+2≥2$\sqrt{({x}^{2}+1)•\frac{1}{{x}^{2}+1}}$+2=4,当且仅当x2+1=$\frac{1}{{x}^{2}+1}$即x=0时取等号,
但题目限制x≠0,故取不到等号,故错误.
故选:C.
点评 本题考查基本不等式求最值,属基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
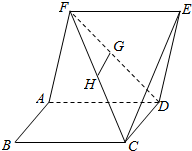 如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.
如图.已知正方形ABCD与ADEF边长都为1,且平面ADEF⊥平面ABCD,G,H是DF,FC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com