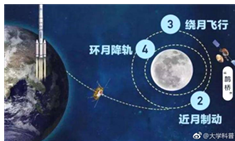
【题目】嫦娥四号月球探测器于2018年12月8日搭载长征三号乙运载火箭在西昌卫星发射中心发射.12日下午4点43分左右，嫦娥四号顺利进入了以月球球心为一个焦点的椭圆形轨道，如图中轨道③所示，其近月点与月球表面距离为
公里，远月点与月球表面距离为
公里.已知月球的直径为
公里，则该椭圆形轨道的离心率约为
A. 
B. 
C. 
D. 
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】如图，在正三棱柱 ABC A1 B1C1 中， AB 3 ， AA1 4 ， M 为 AA1 的中点， P 是 BC 上一点，且由 P 沿棱柱侧面经过棱 CC1 到 M 点的最短路线长为
，设这条最短路线与 CC1 的交点为 N 。求：
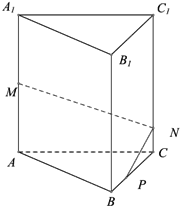
（1）该三棱柱的侧面展开图的对角线长；
（2） PC 和 NC 的长；
（3）平面 NMP 和平面 ABC 所成锐二面角大小的正切值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】物价监督部门为调研某公司新开发上市的一种产品销售价格的合理性，对某公司的该产品的销量与价格进行了统计分析，得到如下数据和散点图：
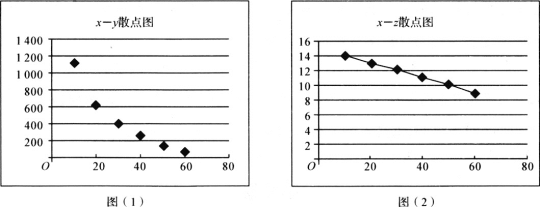
定价x（元／kg） | 10 | 20 | 30 | 40 | 50 | 60 |
年销量y（kg） | 1150 | 643 | 424 | 262 | 165 | 86 |
z＝21ny | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
（参考数据：
，
，
，
）
（Ⅰ）根据散点图判断，y与x和z与x哪一对具有的线性相关性较强（给出判断即可，不必说明理由）？
（Ⅱ）根据（Ⅰ）的判断结果及数据，建立y关于x的回归方程（方程中的系数均保留两位有效数字）．
附：对于一组数据（x1，y1），（x2，y2），（x3，y3），…，（xn，yn），其回归直线
的斜率和截距的最小二乘估计分别为
，
．
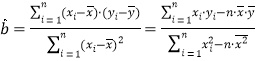查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】椭圆C：
过点M（2，0），且右焦点为F（1，0），过F的直线l与椭圆C相交于A、B两点．设点P（4，3），记PA、PB的斜率分别为k1和k2．
（1）求椭圆C的方程；
（2）如果直线l的斜率等于-1，求出k1k2的值；
（3）探讨k1+k2是否为定值？如果是，求出该定值；如果不是，求出k1+k2的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在
中,已知
，M是BC的中点.
(1)若
,求向量
与向量
的夹角的余弦值；
(2)若O是线段AM上任意一点,且
，求
的最小值；
(3)若点P是边BC上的一点,且
，求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4－4：坐标系与参数方程(本题满分10分)
在平面直角坐标系中，将曲线
向左平移2个单位，再将得到的曲线上的每一个点的横坐标保持不变，纵坐标缩短为原来的
，得到曲线
，以坐标原点
为极点，
轴的正半轴为极轴，建立极坐标系，的极坐标方程为
．
（1）求曲线的参数方程；
（2）已知点
在第一象限，四边形
是曲线的内接矩形，求内接矩形周长的最大值，并求周长最大时点的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左．右焦点分别为
,短轴两个端点为
,且四边形
的边长为
的正方形．
（Ⅰ）求椭圆的方程；
（Ⅱ）若
,分别是椭圆长轴的左,右端点,动点
满足
,连结
,交椭圆于点
．证明: 
的定值；
（Ⅲ）在（Ⅱ）的条件下,试问
轴上是否存在异于点
,的定点
,使得以
为直径的圆恒过直线
,
的交点,若存在,求出点的坐标；若不存在,说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是某地区2012年至2018年生活垃圾无害化处理量（单位：万吨）的折线图.
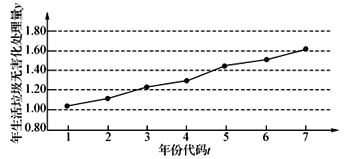
注：年份代码
分别表示对应年份
.
（1）由折线图看出，可用线性回归模型拟合
与
的关系，请用相关系数
（
线性相关较强）加以说明；
（2）建立与的回归方程(系数精确到0.01)，预测2019年该区生活垃圾无害化处理量.
（参考数据）
，
，
，
，
，
，
.
（参考公式）相关系数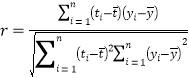
，在回归方程
中斜率和截距的最小二乘估计公式分别为：
，
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
