
【题目】如图所示,四棱锥![]() 的底面是梯形,且
的底面是梯形,且![]() ,
,![]() 平面
平面![]() ,
,![]() 是
是![]() 中点,
中点,![]() .
.
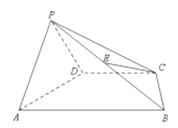
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的高.
的高.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】己知函数![]() .(
.(![]() 是常数,且(
是常数,且(![]() )
)
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 在
在![]() 处取得极值时,若关于
处取得极值时,若关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)求证:当![]() 时
时![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年我省将实施新高考,新高考“依据统一高考成绩、高中学业水平考试成绩,参考高中学生综合素质评价信息”进行人才选拔。我校2018级高一年级一个学习兴趣小组进行社会实践活动,决定对某商场销售的商品A进行市场销售量调研,通过对该商品一个阶段的调研得知,发现该商品每日的销售量![]() (单位:百件)与销售价格
(单位:百件)与销售价格![]() (元/件)近似满足关系式
(元/件)近似满足关系式![]() ,其中
,其中![]() 为常数
为常数![]() 已知销售价格为3元/件时,每日可售出该商品10百件。
已知销售价格为3元/件时,每日可售出该商品10百件。
(1)求函数![]() 的解析式;
的解析式;
(2)若该商品A的成本为2元/件,根据调研结果请你试确定该商品销售价格的值,使该商场每日销售该商品所获得的利润(单位:百元)最大。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=|x﹣m|+|x|,m∈N*,存在实数x使f(x)<2成立.
(1)求不等式f(x)>8的解;
(2)若α,β≥1,f(α)+f(β)=4,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为1的正方体![]() 中,点
中,点![]() 是对角线
是对角线![]() 上的动点(点
上的动点(点![]() 与
与![]() 不重合),则下列结论正确的是____.
不重合),则下列结论正确的是____.
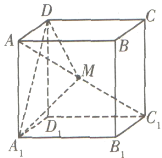
①存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
②存在点![]() ,使得
,使得![]() 平面
平面![]() ;
;
③![]() 的面积不可能等于
的面积不可能等于![]() ;
;
④若![]() 分别是
分别是![]() 在平面
在平面![]() 与平面
与平面![]() 的正投影的面积,则存在点
的正投影的面积,则存在点![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校共有学生2000人,其中男生1100人,女生900人为了调查该校学生每周平均课外阅读时间,采用分层抽样的方法收集该校100名学生每周平均课外阅读时间(单位:小时)
(1)应抽查男生与女生各多少人?
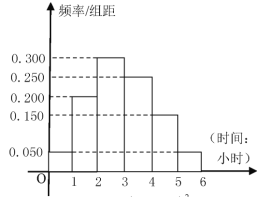
(2)如图,根据收集100人的样本数据,得到学生每周平均课外阅读时间的频率分布直方图,其中样本数据分组区间为![]() .若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
.若在样本数据中有38名女学生平均每周课外阅读时间超过2小时,请完成每周平均课外阅读时间与性别的列联表,并判断是否有95%的把握认为“该校学生的每周平均课外阅读时间与性别有关”.
男生 | 女生 | 总计 | |
每周平均课外阅读时间不超过2小时 | |||
每周平均课外阅读时间超过2小时 | |||
总计 |
附:
| 0.100 | 0.050 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ADEF与梯形ABCD所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
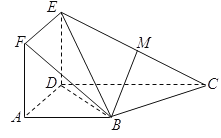
(1)求证:BM∥平面ADEF;
(2)求证:平面BDE⊥平面BEC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com