
【题目】一个盒子中装有6张卡片,上面分别写着如下六个定义域为![]() 的函数:
的函数:![]() ,
, ![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() 从盒子中任取2张卡片,将卡片上的函数相乘得到一个新函数,所得新函数为奇函数的概率是 __________.
从盒子中任取2张卡片,将卡片上的函数相乘得到一个新函数,所得新函数为奇函数的概率是 __________.
科目:高中数学 来源: 题型:
【题目】《张丘建算经》是中国古代数学名著.书中有如下问题;“今有十等人大官甲等十人.宫赐金依次差降之.上三人先入,得金四斤,持出;下四人后入,得金三斤,持出;中央三人未到者,亦依等次更给.问各得金几何及未到三人复应得金几何.”其意思为:“宫廷依次按照等差数列赏赐甲乙丙丁戊己庚辛壬癸十位官员,前面甲乙丙三人进来,共领到四斤黄金之后,便拿着离开了;接着庚辛壬癸四人共领到三斤黄金后,也拿着离开了;中间丁戊己三人没到,也要按照应分得的数量留给他们.问这十人各得黄金多少,并问没到的三人共应该得到多少黄金.”丁戊己三人共应得黄金的斤数为( )
A.3B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强学生的安全意识,某校组织了一次全校2500名学生都参加的“安全知识”考试,阅卷后,学校随机抽取了100份考卷进行分析统计,发现考试成绩(x分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.请根据图表提供的信息,解答下列问题:
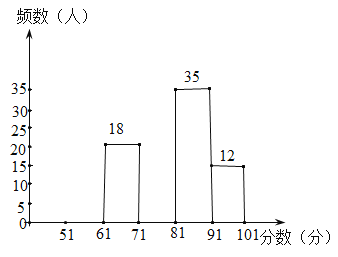

(1)填空:![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)将频数分布直方图补充完整;
(3)该校对考试成绩为![]() 的学生进行奖励,按成绩从高分到低分设一二三等奖,并且一二三等奖的人数比例为1:3:6,请你估算全校获得二等奖的学生人数.
的学生进行奖励,按成绩从高分到低分设一二三等奖,并且一二三等奖的人数比例为1:3:6,请你估算全校获得二等奖的学生人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,点
,点![]() 是椭圆上的一个动点,
是椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若![]() 是椭圆上不重合的四点,
是椭圆上不重合的四点,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,且
,且![]() ,求此时直线
,求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的最小正周期为
的最小正周期为![]() ,且其图象关于直线
,且其图象关于直线![]() 对称,则在下面结论中正确的个数是__________.
对称,则在下面结论中正确的个数是__________.
①图象关于点![]() 对称;②图象关于点
对称;②图象关于点![]() 对称;③在
对称;③在![]() 上是增函数;④在
上是增函数;④在![]() 上是增函数;⑤由
上是增函数;⑤由![]() 可得
可得![]() 必是
必是![]() 的整数倍.
的整数倍.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com