
【题目】已知函数f(x)=lg(ax2+ax+2)(a∈R).
(1)若a=﹣1,求f(x)的单调区间;
(2)若函数f(x)的定义域为R,求实数a的取值范围.
【答案】
(1)
解:当a=﹣1时,f(x)=lg(﹣x2﹣x+2),
由﹣x2﹣x+2>0,即x2+x﹣2<0,解得:﹣2<x<1,
所以函数f(x)的定义域为(﹣2,1);
设t(x)=﹣x2﹣x+2,x∈(﹣2,1),
则y=lgt在t∈(0,+∞)为增函数.
由复合函数的单调性,
f(x)的单调区间与t(x)=﹣x2﹣x+2,x∈(﹣2,1)的单调区间一致.
二次函数t(x)=﹣x2﹣x+2,x∈(﹣2,1)的对称轴为 ![]()
所以t(x)在 ![]() 单调递增,在
单调递增,在 ![]() 单调递减.
单调递减.
所以f(x)的单调增区间为 ![]() ,单调减区间为
,单调减区间为 ![]()
(2)
解:当a=0时,f(x)=lg2为常数函数,定义域为R,满足条件.
当a≠0时,f(x)的定义域为R等价于ax2+ax+2>0恒成立.
于是有 ![]() ,解得:0<a<8
,解得:0<a<8
综上所述,实数a的取值范围是0≤a<8
【解析】(1)将a=﹣1代入f(x),求出f(x)的定义域,结合二次函数的单调性,求出复合函数的单调区间即可;(2))f(x)的定义域为R等价于ax2+ax+2>0恒成立,根据二次函数的性质求出a的范围即可.
【考点精析】关于本题考查的二次函数的性质,需要了解当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能得出正确答案.
上递减才能得出正确答案.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,底面ABCD是菱 形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
中,底面ABCD是菱 形,PA=PB,且侧面PAB⊥平面ABCD,点E是AB的中点.
(1)求证:PE⊥AD;
(2)若CA=CB,求证:平面PEC⊥平面PAB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请阅读下列材料:若两个正实数a1 , a2满足a12+a22=1,那么a1+a2 ![]() .证明:构造函数f(x)=(x﹣a1)2+(x﹣a2)2=2x2﹣2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以△≤0,从而得4(a1+a2)2﹣8≤0,所以a1+a2
.证明:构造函数f(x)=(x﹣a1)2+(x﹣a2)2=2x2﹣2(a1+a2)x+1,因为对一切实数x,恒有f(x)≥0,所以△≤0,从而得4(a1+a2)2﹣8≤0,所以a1+a2 ![]() .根据上述证明方法,若n个正实数满足a12+a22+…+an2=1时,你能得到的结论为 .
.根据上述证明方法,若n个正实数满足a12+a22+…+an2=1时,你能得到的结论为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,平面A1BC⊥侧面A1ABB1 , 且AA1=AB=2 
(1)求证:AB⊥BC;
(2)若AC=2 ![]() ,求锐二面角A﹣A1C﹣B的大小.
,求锐二面角A﹣A1C﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,二面角α﹣l﹣β的大小为60°,A∈β,C∈α,且AB、CD都垂直于棱l,分别交棱l于B、D.已知BD=1,AB=2,CD=3,则AC= . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长时间用手机上网严重影响着学生的身体健康,某校为了解A、B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字). 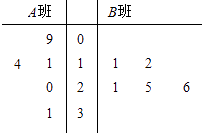
(Ⅰ)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;
(Ⅱ)从A班的样本数据中随机抽取一个不超过19的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com