
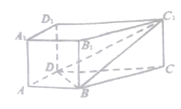
【题目】如图,四棱柱![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ,若存在,请确定点
,若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在点![]() 是
是![]() 的中点,使
的中点,使![]() 平面
平面![]() .
.
【解析】试题分析:(1)先由棱柱的性质证明![]() ,再根据勾股定理可得
,再根据勾股定理可得![]() ,从而可得
,从而可得![]() 平面
平面![]() ,进而根据面面垂直的判定定理即可证明平面
,进而根据面面垂直的判定定理即可证明平面![]() 平面
平面![]() ;(2)存在点
;(2)存在点![]() 是
是![]() 的中点,使
的中点,使![]() 平面
平面![]() ,先根据中位线定理及平行四边形的性质可得
,先根据中位线定理及平行四边形的性质可得![]() ,根据线面平行的判定定理进行证明可得到结论.
,根据线面平行的判定定理进行证明可得到结论.
试题解析:(1)因为![]() 底面
底面![]() , 所以
, 所以![]() 底面
底面![]() ,因为
,因为![]() 底面
底面![]() ,
,
所以![]() 因为底面
因为底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]()
因为![]() ,所以
,所以![]() ,
,![]() 所以
所以![]() ,
,![]()
所以在![]() 中,
中,![]() 所以
所以![]() 所以
所以![]()
又因为![]() 所以
所以![]() 平面
平面![]() 因为
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
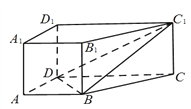
(2)存在点![]() 是
是![]() 的中点,使
的中点,使![]() 平面
平面![]() .
.
证明如下:取线段![]() 的中点为点
的中点为点![]() ,连结
,连结![]() ,所以
,所以![]() ,且
,且![]() 因为
因为![]() ,
,![]() 所以
所以![]() ,且
,且![]() 所以四边形
所以四边形![]() 是平行四边形.所以
是平行四边形.所以![]()
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
【方法点晴】本题主要考查线面平行的判定定理、线面垂直与面面垂直的判定,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,直线y=x+2过椭圆C的左焦点F1.
,直线y=x+2过椭圆C的左焦点F1.
(1)求椭圆C的标准方程;
(2)设过点A(0,﹣1)的直线l与椭圆交于不同两点M、N,当△MON的面积为![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:已知函数f(x)在[m,n](m<n)上的最小值为t,若t≤m恒成立,则称函数f(x)在[m,n](m<n)上具有“DK”性质.例如函数 ![]() 在[1,9]上就具有“DK”性质.
在[1,9]上就具有“DK”性质.
(1)判断函数f(x)=x2﹣2x+2在[1,2]上是否具有“DK”性质?说明理由;
(2)若g(x)=x2﹣ax+2在[a,a+1]上具有“DK”性质,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现如今网上购物已经习以为常,变成人们日常生活的一部分,冲击着人们的传统消费习惯、思维和生活方式,以其特殊的优势而逐渐深入人心.某市场调研机构对在“双十一”购物的![]() 名年龄在
名年龄在![]() 岁的消费者进行了年龄段和性别分布的调查,其部分结果统计如下表:
岁的消费者进行了年龄段和性别分布的调查,其部分结果统计如下表:
年龄(岁) |
|
|
|
|
|
女 | 70 | 50 | 40 | 30 | 20 |
男 | 30 |
| 20 | 15 | 10 |
(1)若按年龄用分层抽样的方法抽取84个人,其中在![]() 内抽取了36人,求
内抽取了36人,求![]() 的值.
的值.
(2)在(1)的条件下,用分层抽样的方法在![]() 岁的消费者中抽取一个容量为8的本,将该样本看成一个总体,从中任取3人,记
岁的消费者中抽取一个容量为8的本,将该样本看成一个总体,从中任取3人,记![]() 表示抽得女性消费者的人数,求随机变量
表示抽得女性消费者的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(log2x)=x2+2x.
(1)求函数f(x)的解析式;
(2)若方程f(x)=a2x﹣4在区间(0,2)内有两个不相等的实根,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)已知递增等差数列![]() 中的
中的![]() 是函数
是函数![]() 的两个零点.数列
的两个零点.数列![]() 满足,点
满足,点![]() 在直线
在直线![]() 上,其中
上,其中![]() 是数列
是数列![]() 的前
的前![]() 项和.
项和.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)令![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com