
【题目】某农场有一块等腰直角三角形的空地![]() ,其中斜边
,其中斜边![]() 的长度为400米.为迎接“五一”观光游,欲在边界
的长度为400米.为迎接“五一”观光游,欲在边界![]() 上选择一点
上选择一点![]() ,修建观赏小径
,修建观赏小径![]() ,其中
,其中![]() 分别在边界
分别在边界![]() 上,小径
上,小径![]() 与边界
与边界![]() 的夹角都为
的夹角都为![]() .区域
.区域![]() 和区域
和区域![]() 内种植郁金香,区域
内种植郁金香,区域![]() 内种植月季花.
内种植月季花.

(1)探究:观赏小径![]() 与
与![]() 的长度之和是否为定值?请说明理由;
的长度之和是否为定值?请说明理由;
(2)为深度体验观赏,准备在月季花区域内修建小径![]() ,当
,当![]() 点在何处时,三条小径
点在何处时,三条小径![]() 的长度和最小?
的长度和最小?
科目:高中数学 来源: 题型:
【题目】如图,曲线![]() 是以原点O为中心、
是以原点O为中心、![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以O为顶点、
是以O为顶点、![]() 为焦点的抛物线的一部分,A是曲线
为焦点的抛物线的一部分,A是曲线![]() 和
和![]() 的交点且
的交点且![]() 为钝角,若
为钝角,若![]() ,
,![]() .
.

(1)求曲线![]() 和
和![]() 的方程;
的方程;
(2)过![]() 作一条与
作一条与![]() 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线![]() 依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问
依次交于B、C、D、E四点,若G为CD中点、H为BE中点,问![]() 是否为定值?若是求出定值;若不是说明理由.
是否为定值?若是求出定值;若不是说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,侧面PAB⊥底面ABCD,底面ABCD为矩形,PA=PB,O为AB的中点,OD⊥PC.

(Ⅰ) 求证:OC⊥PD;
(II)若PD与平面PAB所成的角为30°,求二面角D-PC-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年初,新冠肺炎疫情袭击全国,对人民生命安全和生产生活造成严重影响.在党和政府强有力的抗疫领导下,我国控制住疫情后,一方面防止境外疫情输入,另一方面逐步复工复产,减轻经济下降对企业和民众带来的损失.为降低疫情影响,某厂家拟在2020年举行某产品的促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元(
万元(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(此处每件产品年平均成本按
为常数),如果不搞促销活动,则该产品的年销售量只能是2万件.已知生产该产品的固定投入为8万元,每生产一万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(此处每件产品年平均成本按![]() 元来计算)
元来计算)
(1)将2020年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米两斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=4(单位:升),则输入k的值为( )

A. 10 B. 12 C. 14 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知具有线性相关关系的两个变量![]() 之间的几组数据如下表所示:
之间的几组数据如下表所示:
| 2 | 4 | 6 | 8 | 10 |
| 3 | 6 | 7 | 10 | 12 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计当
,并估计当![]() 时,
时, ![]() 的值;
的值;
(2)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求恰有1个点落在直线![]() 右下方的概率.
右下方的概率.
参考公式: 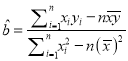 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的一个焦点
的一个焦点![]() 与抛物线
与抛物线![]() 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为![]() .
.
(1)求该椭圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,且点
两点,且点![]() 恰为弦
恰为弦![]() 的中点,求直线
的中点,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com