练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．函数f（x）=（-2）x-x+1．当x依次取前6个自然数时，f（x）的函数值列是{-2，3，-10，13，-36，59}．

    分析 在f（x）=（-2）x-x+1．分别求出当x的值为1，2，3，4，5，6时的函数值，由此能求出结果．

    解答 解：∵函数f（x）=（-2）x-x+1．
    ∴f（1）=（-2）-1+1=-2，
    f（2）=（-2）2-2+1=3，
    f（3）=（-2）3-3+1=-10，
    f（4）=（-2）4-4+1=13，
    f（5）=（-2）5-5+1=-36，
    f（6）=（-2）6-6+1=59．
    ∴当x依次取前6个自然数时，f（x）的函数值列是{-2，3，-10，13，-36，59}．
    故答案为：{-2，3，-10，13，-36，59}．

    点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．若（ax2+$\frac{1}{\sqrt{x}}$）5的展开式中x5的系数是80，则实数a=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．如图，点E、F分别是正方体ABCD-A1B1C1D1的棱AD、AA1的中点，G是棱CC1上一点．
    （Ⅰ）求证：平面A1B1E⊥平面D1FG；
    （Ⅱ）若AB=2，CG=2-$\sqrt{3}$，M是棱DD1的中点，点N在线段D1G上，MN∥DC，求二面角D1-FN-M的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．长方体ABCD-A1B1C1D1中，AB=4，AA1=3，BC=2，P为A1B1中点，M，N，Q分别为棱AB，AA1，CC1上的点，且AB=4MB，AA1=3AN，CC1=3CQ．
    （Ⅰ）求证：PQ⊥平面PD1N；
    （Ⅱ）求二面角P-D1M-N的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数g（x）=$\frac{\sqrt{x+2}}{x}$，h（x）=x2•$\sqrt{x+2}$，f（x）是g （x）与h（x）的积，求：f（x）解析式，并画出其图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

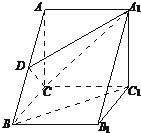    6．如图，三棱柱ABC-A1B1C1中，AC⊥BC，AB⊥BB1，AC=BC=BB1，D为AB的中点，且CD⊥DA1
    （I）求证：BC1∥平面DCA1
    （II）求证：平面ABC⊥平面ABB1A1
    （III）求BC1与平面ABB1A1所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．一直线与直二面角的两个面所成的角分别为α，β，则（　　）
    A．α+β＜90°B．α+β≤90°C．α+β＞90°D．α+β≥90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．如果X～B（1，p），则D（X）（　　）
    A．有最大值$\frac{1}{2}$B．有最大值$\frac{1}{4}$C．有最小值$\frac{1}{2}$D．有最小值$\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．由函数y=sin（5x+$\frac{π}{6}$）的图象得到y=sinx的图象，下列操作正确的是（　　）
    A．将y=sin（5x+$\frac{π}{6}$）的图象向右平移$\frac{π}{30}$；再将所有点的横坐标伸长为原来的5倍，纵坐标不变
    B．将y=sin（5x+$\frac{π}{6}$）的图象向左平移$\frac{π}{30}$；再将所有点的横坐标伸长为原来的5倍，纵坐标不变
    C．将y=sin（5x+$\frac{π}{6}$）的图象向右平移$\frac{π}{30}$；再将所有点的横坐标缩短为原来的$\frac{1}{5}$倍，纵坐标不变
    D．将y=sin（5x+$\frac{π}{6}$）的图象向左平移$\frac{π}{30}$；再将所有点的横坐标缩短为原来的$\frac{1}{5}$倍，纵坐标不变

    查看答案和解析>>

    同步练习册答案