
【题目】随着我国经济的高速发展,汽车的销量也快速增加,每年因道路交通安全事故造成伤亡人数超过![]() 万人,根据国家质量监督检验检疫局发布的《车辆驾驶人员血液、呼气酒精含量阀值与检验》(
万人,根据国家质量监督检验检疫局发布的《车辆驾驶人员血液、呼气酒精含量阀值与检验》(![]() -醉驾车的测试
-醉驾车的测试![]() )的规定:饮酒驾车是指车辆驾驶人员血液中的酒精含量大于或者等于
)的规定:饮酒驾车是指车辆驾驶人员血液中的酒精含量大于或者等于![]() ,小于
,小于![]() 的驾驶行为;醉酒驾车是指车辆驾驶人员血液中的酒精含量大于或者等于
的驾驶行为;醉酒驾车是指车辆驾驶人员血液中的酒精含量大于或者等于![]() 的驾驶行为,某市交通部门从
的驾驶行为,某市交通部门从![]() 年饮酒后驾驶机动车辆发生交通事故的驾驶员中随机抽查了
年饮酒后驾驶机动车辆发生交通事故的驾驶员中随机抽查了![]() 人进行统计,得到如下数据:
人进行统计,得到如下数据:
酒精含量
|
|
|
|
|
|
发生交通事故的人数 |
|
|
|
|
|
已知从这![]() 人中任意抽取两人,两人均是醉酒驾车的概率是
人中任意抽取两人,两人均是醉酒驾车的概率是![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)实践证明,驾驶人员血液中的酒精含量与发生交通事故的人数具有线性相关性,试建立![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)试预测,驾驶人员血液中的酒精含量为多少时,发生交通事故的人数会超过取样人数的![]() ?
?
参考数据:![]() ,
,
回归直线方程![]() 中系数计算公式
中系数计算公式 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志是“连续10天,每天新增疑似病例不超过7人”,根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A. 甲地:总体均值为3,中位数为4
B. 乙地:总体均值为1,总体方差大于0
C. 丙地:总体均值为2,总体方差为3
D. 丁地:中位数为2,众数为3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市教育局卫生健康所对全市高三年级的学生身高进行抽样调查,随机抽取了100名学生,他们身高都处于![]() 五个层次,根据抽样结果得到如下统计图表,则从图表中不能得出的信息是( )
五个层次,根据抽样结果得到如下统计图表,则从图表中不能得出的信息是( )
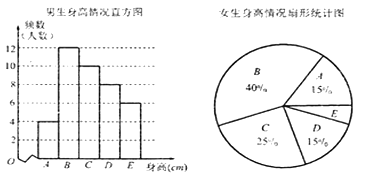
A. 样本中男生人数少于女生人数
B. 样本中![]() 层次身高人数最多
层次身高人数最多
C. 样本中![]() 层次身高的男生多于女生
层次身高的男生多于女生
D. 样本中![]() 层次身高的女生有3人
层次身高的女生有3人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,
所在的平面互相垂直, ![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

(Ⅰ) 若点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ) 求证:平面![]() 平面
平面![]() ;
;
(Ⅲ) 当平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,直线
,直线![]() 不经过椭圆上顶点
不经过椭圆上顶点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() ,
,![]() 不同两点.
不同两点.
(1)当![]() ,
,![]() 时,求椭圆
时,求椭圆![]() 的离心率的取值范围;
的离心率的取值范围;
(2)若![]() ,直线
,直线![]() 与
与![]() 的斜率之和为
的斜率之和为![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生会为了解高二年级600名学生课余时间参加中华传统文化活动的情况(每名学生最多参加7场).随机抽取50名学生进行调查,将数据分组整理后,列表如下:

则以下四个结论中正确的是( )
A.表中![]() 的数值为10
的数值为10
B.估计该年级参加中华传统文化活动场数不高于2场的学生约为108人
C.估计该年级参加中华传统文化活动场数不低于4场的学生约为216人
D.若采用系统抽样方法进行调查,从该校高二600名学生中抽取容量为30的样本,则分段间隔为15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知位于![]() 轴左侧的圆
轴左侧的圆![]() 与
与![]() 轴相切于点
轴相切于点![]() 且被
且被![]() 轴分成的两段圆弧长之比为
轴分成的两段圆弧长之比为![]() ,直线
,直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() .
.

(1)求圆![]() 的方程;
的方程;
(2)求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在几何体中,四边形![]() 为菱形,对角线
为菱形,对角线![]() 与
与![]() 的交点为
的交点为![]() ,四边形
,四边形![]() 为梯形,
为梯形,![]() ,
,![]() .
.
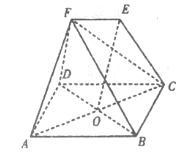
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)若![]() ,求
,求![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com