
【题目】对于曲线![]() 所在的平面上的定点
所在的平面上的定点![]() ,若存在以点
,若存在以点![]() 为顶点的角
为顶点的角![]() ,使得
,使得![]() 对于曲线
对于曲线![]() 上的任意两个不同的点
上的任意两个不同的点![]() 恒成立,则称角
恒成立,则称角![]() 为曲线
为曲线![]() 的“
的“![]() 点视角”,并称其中最小的“
点视角”,并称其中最小的“![]() 点视角”为曲线
点视角”为曲线![]() 相对于点
相对于点![]() 的”
的”![]() 点确视角”.已知曲线
点确视角”.已知曲线![]() 和圆
和圆![]() 是
是![]() 轴上一点
轴上一点
(1)对于坐标原点![]() ,写出曲线
,写出曲线![]() 的“
的“![]() 点确视角”的大小;
点确视角”的大小;
(2)若![]() 在曲线
在曲线![]() 上,求
上,求![]() 的最小值;
的最小值;
(3)若曲线![]() 和圆
和圆![]() 的“
的“![]() 点确视角”相等,求
点确视角”相等,求![]() 点坐标.
点坐标.
【答案】(1)![]() ;(2)
;(2)
![]() ;(3)
;(3)
【解析】
(1)根据“![]() 点确视角”的定义,可知“
点确视角”的定义,可知“![]() 点确视角”即为原点与两条渐近线所成角的大小,结合渐近线方程即可求得该角大小.
点确视角”即为原点与两条渐近线所成角的大小,结合渐近线方程即可求得该角大小.
(2)设出Q点坐标,代入双曲线方程可得Q的横纵坐标的等量关系.根据两点间距离公式即可表示出![]() ,根据Q横坐标的取值范围讨论P点的位置,即可求得
,根据Q横坐标的取值范围讨论P点的位置,即可求得![]() 的最小值.
的最小值.
(3)根据双曲线与圆的“![]() 点确视角”相等,可得与双曲线相切的直线方程,联立后通过判别式即可求得
点确视角”相等,可得与双曲线相切的直线方程,联立后通过判别式即可求得![]() 点坐标.
点坐标.
(1)由题意可知, “![]() 点确视角”即为原点与两条渐近线所成角的大小,
点确视角”即为原点与两条渐近线所成角的大小,
因为曲线![]() ,两条渐近线方程为
,两条渐近线方程为![]()
两条渐近线的倾斜角分别为![]() 与
与![]()
所以两条渐近线的夹角为![]()
即“![]() 点确视角”为
点确视角”为![]()
(2)设![]() ,代入曲线
,代入曲线![]() 方程可得
方程可得
![]() ,化简即为
,化简即为![]()
因为![]()
则![]()
![]()
![]()

因为![]() 在双曲线右支上,所以
在双曲线右支上,所以![]()
所以当![]() 时,
时, ![]() 则
则![]()
所以当![]() 时,
时, ![]() 则
则![]()
综上可知,
![]()
(3)曲线![]() 和圆
和圆![]()
根据题意将两个曲线画在坐标系中,如下图所示:

因为曲线![]() 和圆
和圆![]() 的“
的“![]() 点确视角”相等
点确视角”相等
由图像可知它们共同的“![]() 点确视角”为钝角
点确视角”为钝角
双曲线的两条渐近线方程为![]()
所以当![]() 时,过P点与双曲线相切时, “
时,过P点与双曲线相切时, “![]() 点确视角”相等
点确视角”相等
则切线方程可表示为![]()
联立双曲线 ,化简得
,化简得![]()
根据相切时![]() 可得
可得![]()
解得![]() 或
或![]()
因为![]()
故


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在本题中,我们把具体如下性质的函数![]() 叫做区间
叫做区间![]() 上的闭函数:①
上的闭函数:①![]() 的定义域和值域都是
的定义域和值域都是![]() ;②
;②![]() 在
在![]() 上是增函数或者减函数.
上是增函数或者减函数.
(1)若![]() 在区间
在区间![]() 上是闭函数,求常数
上是闭函数,求常数![]() 的值;
的值;
(2)找出所有形如![]() 的函数(
的函数(![]() 都是常数),使其在区间
都是常数),使其在区间![]() 上是闭函数.
上是闭函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)(2017·长春市二模)如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 中点.
中点.

(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知常数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)在(1)的条件下,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若数列![]() 中存在三项
中存在三项![]() ,
,![]() ,
,![]() (
(![]() 且
且![]() )依次成等差数列,求
)依次成等差数列,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为
的左、右焦点为![]() 、
、![]() .
.
(1)求以![]() 为焦点,原点为顶点的抛物线方程;
为焦点,原点为顶点的抛物线方程;
(2)若椭圆![]() 上点
上点![]() 满足
满足![]() ,求
,求![]() 的纵坐标
的纵坐标![]() ;
;
(3)设![]() ,若椭圆
,若椭圆![]() 上存在两个不同点
上存在两个不同点![]() 、
、![]() 满足
满足![]() ,证明:直线
,证明:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】贺先生想向银行贷款买辆新能源车,银行可以贷给贺先生N元,一年后需要一次性还1.02N元.
(1)贺先生发现一个投资理财方案:每个月月初投资![]() 元,共投资一年,每月的月收益率达到1%,于是贺先生决定贷款12
元,共投资一年,每月的月收益率达到1%,于是贺先生决定贷款12![]() 元,按投资方案投资,求
元,按投资方案投资,求![]() 的值,使得贺先生用最终投所得的钱还清贷款后,还有120000的余额去旅游(精确到0.01元);
的值,使得贺先生用最终投所得的钱还清贷款后,还有120000的余额去旅游(精确到0.01元);
(2)贺先生又发现一个投资方案:第![]() 个月月初投资
个月月初投资![]() 元
元![]() 共投资一年,每月的月收益率达到1%,则贺先生应贷款多少,使得用最终投资所得的钱还清后,还有120000的余额去旅游(精确到0.01元).
共投资一年,每月的月收益率达到1%,则贺先生应贷款多少,使得用最终投资所得的钱还清后,还有120000的余额去旅游(精确到0.01元).
(参考数据![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象的顶点坐标为
的图象的顶点坐标为![]() ,且过坐标原点
,且过坐标原点![]() .数列
.数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 在二次函数
在二次函数![]() 的图象上.
的图象上.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)在数列![]() 中是否存在这样一些项:
中是否存在这样一些项:![]()
![]()
![]() ,这些项都能够构成以
,这些项都能够构成以![]() 为首项,
为首项,![]() 为公比的等比数列
为公比的等比数列![]() ?若存在,写出
?若存在,写出![]() 关于
关于![]() 的表达式;若不存在,说明理由.
的表达式;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】举行动物运动会其中有小兔大兔接力赛跑一项,跑道从起点![]() 经过点
经过点![]() 再到终点
再到终点![]() ,其中
,其中![]() 米,
米,![]() 米,规定小兔跑第一棒从
米,规定小兔跑第一棒从![]() 到
到![]() ,大兔在
,大兔在![]() 处接力完成跑第二棒从
处接力完成跑第二棒从![]() 到
到![]() ,假定接力赛跑时小兔大兔的各自速度都是均匀的,且它们的速度之和为定值10米/秒,试问小兔和大兔应以怎样的速度接力赛跑,才能使接力赛成绩最好(所需时间最短),并求其最短时间.
,假定接力赛跑时小兔大兔的各自速度都是均匀的,且它们的速度之和为定值10米/秒,试问小兔和大兔应以怎样的速度接力赛跑,才能使接力赛成绩最好(所需时间最短),并求其最短时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如图.
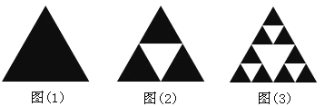
现在上述图(3)中随机选取一个点,则此点取自阴影部分的概率为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com