
【题目】如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE= ![]() AD.
AD. 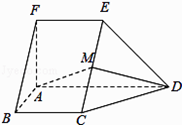
(1)求异面直线BF与DE所成的角的大小;
(2)证明平面AMD⊥平面CDE;
(3)求锐二面角A﹣CD﹣E的余弦值.
【答案】
(1)解:如图所示,建立空间直角坐标系,点A为坐标原点.

设AB=1,依题意得B(1,0,0),C(1,1,0),D(0,2,0),E(0,1,1),F(0,0,1),M( ![]() ,1,
,1, ![]() ).
).
![]() =(﹣1,0,1),
=(﹣1,0,1), ![]() =(0,﹣1,1),
=(0,﹣1,1),
于是cos< ![]() ,
, ![]() >=
>= 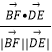 =
= ![]() =
= ![]() .
.
所以异面直线BF与DE所成的角的大小为60°
(2)证明:由 ![]() =(
=( ![]() ,1,
,1, ![]() ),
), ![]() =(﹣1,0,1),
=(﹣1,0,1),
![]() =(0,2,0),可得
=(0,2,0),可得 ![]()
![]() =0,
=0, ![]()
![]() =0.
=0.
因此,CE⊥AM,CE⊥AD.
又AM∩AD=A,故CE⊥平面AMD.
而CE∥平面CDE,所以平面AMD⊥平面CDE
(3)解:设平面CDE的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 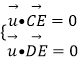 于是
于是 ![]() 令x=1,可得
令x=1,可得 ![]() =(1,1,1).
=(1,1,1).
又由题设,平面ACD的一个法向量为v=(0,0,1).
所以, ![]() =
= ![]() =
= ![]() =
= ![]() .
.
因为二面角A﹣CD﹣E为锐角,所以其余弦值为 ![]()
【解析】(1)建立空间直角坐标系,点A为坐标原点.设AB=1,求出B,C,D,E,F,M.求出 ![]() =(﹣1,0,1),
=(﹣1,0,1), ![]() =(0,﹣1,1),利用空间向量的数量积求解异面直线BF与DE所成的角的大小.(2)证明
=(0,﹣1,1),利用空间向量的数量积求解异面直线BF与DE所成的角的大小.(2)证明 ![]()
![]() =0,
=0, ![]()
![]() =0.推出CE⊥平面AMD.然后证明平面AMD⊥平面CDE.(3)求出平面CDE的法向量为
=0.推出CE⊥平面AMD.然后证明平面AMD⊥平面CDE.(3)求出平面CDE的法向量为 ![]() ,平面ACD的一个法向量为v,利用空间向量的数量积求解二面角的余弦值.
,平面ACD的一个法向量为v,利用空间向量的数量积求解二面角的余弦值.
【考点精析】掌握异面直线及其所成的角和平面与平面垂直的判定是解答本题的根本,需要知道异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;一个平面过另一个平面的垂线,则这两个平面垂直.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可参加抽奖,抽奖有两种方案可供选择. 方案一:从装有4个红球和2个白球的不透明箱中,随机摸出2个球,若摸出的2个球都是红球则中奖,否则不中奖;
方案二:掷2颗骰子,如果出现的点数至少有一个为4则中奖,否则不中奖.(注:骰子(或球)的大小、形状、质地均相同)
(Ⅰ)有顾客认为,在方案一种,箱子中的红球个数比白球个数多,所以中奖的概率大于 ![]() .你认为正确吗?请说明理由;
.你认为正确吗?请说明理由;
(Ⅱ)如果是你参加抽奖,你会选择哪种方案?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sin(x﹣ ![]() )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移
)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移 ![]() 个单位,得到的图象对应的解析式是( )
个单位,得到的图象对应的解析式是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F. 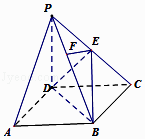
(1)求证PA∥平面EDB;
(2)求二面角C﹣PB﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x2﹣ ![]() 在其定义域内的一个子区间(k﹣1,k+1)内不是单调函数,则实数k的取值范围( )
在其定义域内的一个子区间(k﹣1,k+1)内不是单调函数,则实数k的取值范围( )
A.[1,+∞)
B.[1, ![]() )
)
C.[1,+2)
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,AD⊥平面PAB,△PAB是正三角形,AD=AB=2,BC=1,E是线段AB的中点 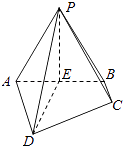
(1)求证:平面PDE⊥平面ABCD;
(2)设直线PC与平面PDE所成角为θ,求cosθ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数 ![]() 的图象,只需将函数y=sin2x的图象上每一点( )
的图象,只需将函数y=sin2x的图象上每一点( )
A.向左平移 ![]() 个单位长度
个单位长度
B.向左平移 ![]() 个单位长度
个单位长度
C.向右平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com