
【题目】某校高三特长班的一次月考数学成绩的茎叶图和频率分布直方图1都受到不同程度的损坏,但可见部分如图2,据此解答如下问题: 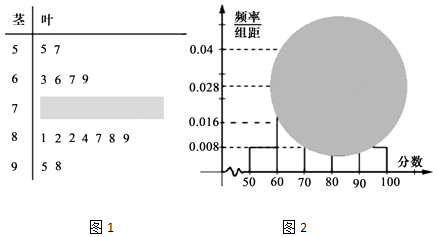
(Ⅰ)求分数在[70,80)之间的频数,并计算频率分布直方图中[70,80)间的矩形的高;
(Ⅱ)若要从分数在[50,70)之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份在[50,60)之间的概率.
【答案】解:(Ⅰ)分数在[50,60)的频率为0.08, 由茎叶图知:分数在[50,60)之间的频率为2,
∴全班人数为 ![]() ,
,
分数在[70,80)之间的频数为10,
分数在[80,90)间的频数为25﹣(2+7+10+2)=4,
∴频率分布直方图中[80,90)间的矩形的高为: ![]() .
.
(Ⅱ)将[80,90)之间的4个分数编号为1,2,3,4,
[80,90)之间的2个分数编号为5,6,
在[80,100)之间的试卷中任取两份的基本事件为:
(1,5),(1,6),(2,5),(2,6),(3,5),
(3,6),(4,5),(4,6),(5,6),共9个,
∴至少有一份在[90,100)之间的概率为p= ![]()
【解析】(Ⅰ)分数在[50,60)的频率为0.08,由茎叶图知:分数在[50,60)之间的频率为2,由此能求出结果.(Ⅱ)将[80,90)之间的4个分数编号为1,2,3,4,[80,90)之间的2个分数编号为5,6,在[80,100)之间的试卷中任取两份,利用列举法能求出至少有一份在[90,100)之间的概率.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的
中点.
(1) 求证: AC⊥BC1
(2) 求证:AC1∥平面CDB1
(3) 求异面直线AC1与B1C所成角的余弦值.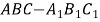
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,侧面PAD⊥底面ABCD,底面ABCD是平行四边形,∠ABC=45°,AD=AP=2, ![]() ,E为CD的中点,点F在线段PB上.
,E为CD的中点,点F在线段PB上. 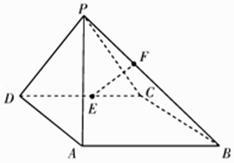
(Ⅰ)求证:AD⊥PC;
(Ⅱ)试确定点F的位置,使得直线EF与平面PDC所成的角和直线EF与平面ABCD所成的角相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 满足:
满足:![]() ,且
,且![]() ,其前n项和
,其前n项和![]() .
.
(1)求证:![]() 为等比数列;
为等比数列;
(2)记![]() 为数列
为数列![]() 的前n项和.
的前n项和.
(i)当![]() 时,求
时,求![]() ;
;
(ii)当![]() 时,是否存在正整数
时,是否存在正整数![]() ,使得对于任意正整数
,使得对于任意正整数![]() ,都有
,都有![]() ?如果存在,求出
?如果存在,求出![]() 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以直角坐标系的原点为极点,以
),以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立坐标系,圆
轴的正半轴为极轴建立坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的直角坐标方程(化为标准方程)及曲线
的直角坐标方程(化为标准方程)及曲线![]() 的普通方程;
的普通方程;
(2)若圆![]() 与曲线
与曲线![]() 的公共弦长为
的公共弦长为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系内,已知![]() 是以点
是以点![]() 为圆心的圆上的一点,折叠该圆两次使点
为圆心的圆上的一点,折叠该圆两次使点![]() 分别与圆上不相同的两点(异于点
分别与圆上不相同的两点(异于点![]() )重合,两次的折痕方程分别为
)重合,两次的折痕方程分别为![]() 和
和![]() ,若圆上存在点
,若圆上存在点![]() ,使得
,使得![]() ,其中点
,其中点![]() 、
、![]() ,则
,则![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD. 求证:(Ⅰ)EF∥平面ABC;
(Ⅱ)AD⊥AC.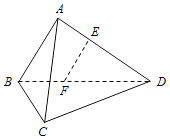
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是样本容量为200的频率分布直方图.根据样本的频率分布直方图估计,样本数落在[6,10]内的频数为 ,数据落在(2,10)内的概率约为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com