
【题目】设抛物线C:y2=4x的焦点为F,过F的直线l与C交于A,B两点,点M的坐标为(﹣1,0).
(1)当l与x轴垂直时,求△ABM的外接圆方程;
(2)记△AMF的面积为S1,△BMF的面积为S2,当S1=4S2时,求直线l的方程.
【答案】(1)x2+y2﹣2x﹣3=0;(2)x![]() y+1
y+1
【解析】
(1)由题意求出![]() ,
,![]() 的坐标,设圆的一般方程,将
的坐标,设圆的一般方程,将![]() ,
,![]() ,
,![]() 坐标代入圆的方程求出参数,即求出圆的方程;(2)由题意得面积之比为纵坐标的绝对值之比,求出坐标的关系,代入抛物线方程,求出
坐标代入圆的方程求出参数,即求出圆的方程;(2)由题意得面积之比为纵坐标的绝对值之比,求出坐标的关系,代入抛物线方程,求出![]() 的方程.
的方程.
(1)由题意得:焦点F(1,0),
当l与x轴垂直时,l的方程:x=1,代入抛物线得A(1,2),B(1,﹣2),
而M(﹣1,0)设△ABMD的外接圆的方程:x2+y2+Dx+Ey+F=0,
所以: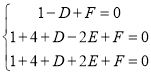 解得:D=﹣2,E=0,F=﹣3,
解得:D=﹣2,E=0,F=﹣3,
所以△ABM的外接圆方程:x2+y2﹣2x﹣3=0;
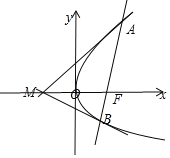
(2)由题意的直线l的斜率不为零,设直线l的方程:x=my+1,A(x,y),B(x',y'),
设A在x轴上方,联立抛物线的方程可得y2﹣4my﹣4=0,y+y'=4m,
由题意知:y=﹣4y',
∴y'![]() ,代入直线得x'
,代入直线得x'![]() 1,B在抛物线上,
1,B在抛物线上,
所以:(![]() )2﹣4(
)2﹣4(![]() 1)=0,解得m
1)=0,解得m![]() ,
,
所以直线l的方程:x![]() y+1.
y+1.


科目:高中数学 来源: 题型:
【题目】下列四个命题中真命题是![]()
![]()
A. 同垂直于一直线的两条直线互相平行
B. 底面各边相等,侧面都是矩形的四棱柱是正四棱柱
C. 过空间任一点与两条异面直线都垂直的直线有且只有一条
D. 过球面上任意两点的大圆有且只有一个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,已知椭圆 C:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,且过点
,且过点![]() ,点P在第四象限, A为左顶点, B为上顶点, PA交y轴于点C,PB交x轴于点D.
,点P在第四象限, A为左顶点, B为上顶点, PA交y轴于点C,PB交x轴于点D.
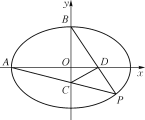
(1) 求椭圆 C 的标准方程;
(2) 求 △PCD 面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着高考制度的改革,某省即将实施“语数外+3”新高考的方案,2019年秋季入学的高一新生将面临从物理(物)、化学(化)、生物(生)、政治(政)、历史(历)、地理(地)六科中任选三科(共20种选法)作为自己将来高考“语数外+3”新高考方案中的“3”某市为了顺利地迎接新高考改革,在某高中200名学生中进行了“学生模拟选科数据”调查,每个学生只能从表格中的20种课程组合中选择一种学习模拟选课数据统计如下表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
组合学科 | 物化生 | 物化政 | 物化历 | 物化地 | 物生政 | 物生历 | 物生地 | 物政历 | 物政地 | 物历地 |
人数 | 20人 | 5人 | 10人 | 10人 | 5人 | 15人 | 10人 | 5人 | 0人 | 5人 |
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 合计 |
化生政 | 化生历 | 化生地 | 化政历 | 化政地 | 化历地 | 生政历 | 生政地 | 生历地 | 政历地 | |
5人 | … | … | … | … | … | 10人 | 5人 | … | 25人 | 200人 |
为了解学生成绩与学生模拟选课情况之问的关系,用分层抽样的方法从这200名学生中抽取40人的样本进行分析
(l)样本中选择组合20号“政历地”的有多少人?若以样本频率作为概率,求该高中学生不选物理学科的概率?
(Ⅱ)从样本中选择学习生物且学习政治的学生中随机抽取3人,求这3人中至少有一人还学习历史的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(3)若函数![]() 有两个极值点
有两个极值点![]() ,若过两点
,若过两点![]() 的直线
的直线![]() 与
与![]() 轴的交点在曲线
轴的交点在曲线![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点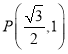 ,且长轴长是短轴长的2倍.
,且长轴长是短轴长的2倍.
(1)求椭圆的标准方程;
(2)若点![]() 在椭圆上运动,点
在椭圆上运动,点![]() 在圆
在圆![]() 上运动,且总有
上运动,且总有![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)过点![]() 的动直线
的动直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,试问:在此坐标平面上是否存在一个点
两点,试问:在此坐标平面上是否存在一个点![]() ,使得无论
,使得无论![]() 如何转动,以
如何转动,以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标;若不存在,请说明由.
的坐标;若不存在,请说明由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com