
【题目】设![]() 实数
实数![]() 满足不等式
满足不等式![]() 函数
函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知“![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求正整数
的必要不充分条件,求正整数![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:由![]() ,得
,得![]() ;函数
;函数![]() 无极值点,
无极值点,![]() 恒成立,得
恒成立,得![]() ,解得
,解得![]() .(1)“
.(1)“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,则
”为真命题,则![]() 与
与![]() 只有一个命题是真命题,分成
只有一个命题是真命题,分成![]() 真
真![]() 假和
假和![]() 假
假![]() 真两类来求
真两类来求![]() 的取值范围;(2)“
的取值范围;(2)“![]() ”为真命题,两个都是真命题,所以
”为真命题,两个都是真命题,所以![]() .将
.将![]() 因式分解得
因式分解得![]() ,解得
,解得![]() 或
或![]() ,
,![]() ,
,![]() 是
是![]() 的必要不充分条件得
的必要不充分条件得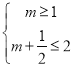 ,解得
,解得![]() ,所以
,所以![]() .
.
试题解析:
由![]() ,得
,得![]() ,即
,即![]() ................1分
................1分
∵函数![]() 无极值点,∴
无极值点,∴![]() 恒成立,得
恒成立,得![]() ,解得
,解得![]() ,
,
即![]() ..................................3分
..................................3分
(1)∵“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,∴
”为真命题,∴![]() 与
与![]() 只有一个命题是真命题.
只有一个命题是真命题.
若![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() ;.....................5分
;.....................5分
若![]() 为真命题,
为真命题,![]() 为假命题,则
为假命题,则![]() ..............6分
..............6分
于是,实数![]() 的取值范围为
的取值范围为![]() .....................7分
.....................7分
(2)∵“![]() ”为真命题,∴
”为真命题,∴![]() ..............8分
..............8分
又![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,...................10分
,...................10分
即![]() 或
或![]() ,从而
,从而![]() ,
,
∵![]() 是
是![]() 的必要不充分条件,即
的必要不充分条件,即![]() 是
是![]() 的充分不必要条件,
的充分不必要条件,
∴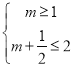 ,解得
,解得![]() ,∵
,∵![]() ,∴
,∴![]() ..................12分
..................12分


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a2=5,S5=40.等比数列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通项公式
(2)令cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,四边形
,四边形![]() 为正方形,点
为正方形,点![]() 分别为线段
分别为线段![]() 上的点,
上的点,![]() .
.
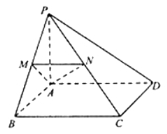
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:当点![]() 不与点
不与点![]() 重合时,
重合时,![]() 平面
平面![]() ;
;
(3)当![]() ,
,![]() 时,求点
时,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,四边形ABCD是矩形,侧面PAD⊥底面ABCD,若点E,F分别是PC,BD的中点。
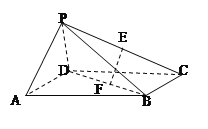
(1)求证:EF∥平面PAD;
(2)求证:平面PAD⊥平面PCD
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() , 若
, 若![]() 成等比数列,椭圆
成等比数列,椭圆![]() 上的点到焦点
上的点到焦点![]() 的最短距离为
的最短距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为直线
为直线![]() 上任意一点,过
上任意一点,过![]() 的直线交椭圆
的直线交椭圆![]() 于点
于点![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体ABCD中,截面PQMN是正方形,则下列命题中,正确的为________ (填序号).
①AC⊥BD;②AC∥截面PQMN;③AC=BD;④异面直线PM与BD所成的角为45°.
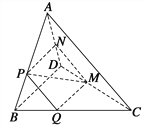
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度)以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如下图示.
(Ⅰ)求直方图中x的值;
(Ⅱ)求月平均用电量的众数和中位数;
(Ⅲ)在月平均用电量为[220,240),[240,260),[260,280)的三组用户中,用分层抽样的方法抽取10户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
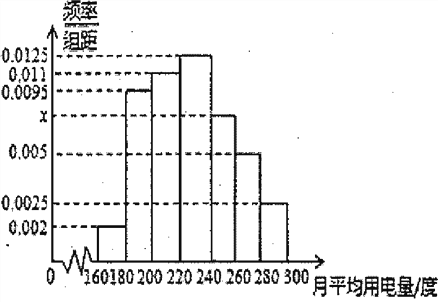
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com