
A、4
| ||
| B、8π | ||
C、8
| ||
| D、24π |
| 3 |
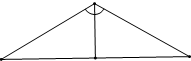 r=
r=| 3 |
| d2+h2 |
| 1 |
| 2 |
| d2+h2 |
| r2-x2+h2 |
| 4h2-x2 |
| x2(4h2-x2) |
| x2+4h2-x2 |
| 2 |
| 2 |
| 3 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
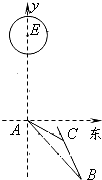 在特定时段内,以点E为中心的5海里以内海域被设为警戒水域.点E正南30海里处有一个雷达观测点A.某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20
在特定时段内,以点E为中心的5海里以内海域被设为警戒水域.点E正南30海里处有一个雷达观测点A.某时刻测得一艘匀速直线行驶的船只位于点A南偏东45°且与点A相距20| 2 |
| 5 | ||
|
| π |
| 2 |
| 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| z |
| ω |
| z |
| ω |
| z |
| ω |
| z |
| ω |
| z |
| ω |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、8 | B、16 | C、32 | D、64 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| A、y=-3x-3 |
| B、y=-3x+3 |
| C、y=-3x-1 |
| D、y=3x-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com