
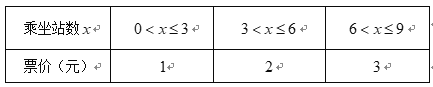
【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过
站的地铁票价如下表:现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站,且他们各自在每个站下车的可能性是相同的.
站,且他们各自在每个站下车的可能性是相同的.
(1)若甲、乙两人共付费![]() 元,则甲、乙下车方案共有多少种?
元,则甲、乙下车方案共有多少种?
(2)若甲、乙两人共付费![]() 元,求甲比乙先到达目的地的概率.
元,求甲比乙先到达目的地的概率.
【答案】(1)9;(2)![]()
【解析】
(1)由题意知甲、乙乘坐地铁均不超过![]() 站,前
站,前![]() 站设为
站设为![]() ,
, ![]() ,
, ![]() ,(2),甲、乙两人共有
,(2),甲、乙两人共有![]() 种下车方案;(2)设
种下车方案;(2)设![]() 站分别为
站分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,因为甲、乙两人共付费
,因为甲、乙两人共付费![]() 元,共有甲付
元,共有甲付![]() 元,乙付
元,乙付![]() 元;甲付
元;甲付![]() 元,乙付
元,乙付![]() 元;甲付
元;甲付![]() 元,乙付
元,乙付![]() 元三类情况. 由(1)可知每类情况中有
元三类情况. 由(1)可知每类情况中有![]() 种方案,所以甲、乙两人共付费
种方案,所以甲、乙两人共付费![]() 元共有
元共有![]() 种方案. 而甲比乙先到达目的地的方案有共
种方案. 而甲比乙先到达目的地的方案有共![]() 种,从而得到甲比乙先到达目的地的概率.
种,从而得到甲比乙先到达目的地的概率.
(1)由题意知甲、乙乘坐地铁均不超过![]() 站,前
站,前![]() 站设为
站设为![]() ,
, ![]() ,
, ![]() ,
,
甲、乙两人共有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() 种下车方案.
种下车方案.
(2)设![]() 站分别为
站分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,因为甲、乙两人共付费
,因为甲、乙两人共付费![]() 元,共有甲付
元,共有甲付![]() 元,乙付
元,乙付![]() 元;甲付
元;甲付![]() 元,乙付
元,乙付![]() 元;甲付
元;甲付![]() 元,乙付
元,乙付![]() 元三类情况.
元三类情况.
由(1)可知每类情况中有![]() 种方案,所以甲、乙两人共付费
种方案,所以甲、乙两人共付费![]() 元共有
元共有![]() 种方案.
种方案.
而甲比乙先到达目的地的方案有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共
,共![]() 种,
种,
故所求概率为![]() .
.
所以甲比乙先到达目的地的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】针对“中学生追星问题”,某校团委对“学生性别和中学生追星是否有关”作了一次调查,其中女生人数是男生人数的![]() ,男生追星的人数占男生人数的
,男生追星的人数占男生人数的![]() ,女生追星的人数占女生人数的
,女生追星的人数占女生人数的![]() .若有
.若有![]() 的把握认为是否追星和性别有关,则男生至少有( )
的把握认为是否追星和性别有关,则男生至少有( )
参考数据及公式如下:
|
|
|
|
|
|
|
|
![]()
A. 12B. 11C. 10D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,
,![]() 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为![]() .
.
(1)求![]() 的方程;
的方程;
(2)过![]() 的左焦点
的左焦点![]() 作直线
作直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() (
(![]() 为坐标原点)与直线
为坐标原点)与直线![]() 相交于点
相交于点![]() ,是否存在直线
,是否存在直线![]() 使得
使得![]() 为等腰直角三角形,若存在,求出
为等腰直角三角形,若存在,求出![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
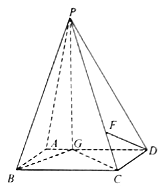
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() 在平面
在平面![]() 上的射影为
上的射影为![]() ,且
,且![]() 在
在![]() 上,且
上,且![]() ,
,![]() ,
,![]() 是
是![]() 的中点,四面体
的中点,四面体![]() 的体积为
的体积为![]() .
.
(Ⅰ)求异面直线![]() 与
与![]() 所成的角余弦值;
所成的角余弦值;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离;
的距离;
(Ⅲ)若![]() 点是棱
点是棱![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系平面![]() 上的一列点
上的一列点![]() ,
,![]() ,…,
,…,![]() ,记为
,记为![]() ,若由
,若由![]() 构成的数列
构成的数列![]() 满足
满足![]() ,
,![]() ,其中
,其中![]() 为与
为与![]() 轴正方向相同的单位向量,则称
轴正方向相同的单位向量,则称![]() 为
为![]() 点列.
点列.
(1)判断![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,是否为
,是否为![]() 点列,并说明理由;
点列,并说明理由;
(2)若![]() 为
为![]() 点列.且点
点列.且点![]() 在点
在点![]() 的右上方,(即
的右上方,(即![]() )任取其中连续三点
)任取其中连续三点![]() ,
,![]() ,
,![]() 判断
判断![]() 的形状(锐角三角形,直角三角形,钝角三角形),并给予证明;
的形状(锐角三角形,直角三角形,钝角三角形),并给予证明;
(3)若![]() 为
为![]() 点列,正整数
点列,正整数![]() ,满足
,满足![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国明代珠算家程大位的名著《直指算法统宗》中有如下问题:“今有白米一百八十石,令三人从上及和减率分之,只云甲多丙米三十六石,问:各该若干?”其意思为:“今有白米一百八十石,甲、乙、丙三人来分,他们分得的白米数构成等差数列,只知道甲比丙多分三十六石,那么三人各分得多少白米?”请问:乙应该分得( )白米
A. 96石B. 78石C. 60石D. 42石
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两种树苗中各抽测了10株树苗的高度,其茎叶图如图.根据茎叶图,下列描述正确的是( )
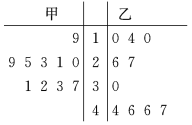
A.甲种树苗的平均高度大于乙种树苗的平均高度,且甲种树苗比乙种树苗长得整齐
B.甲种树苗的平均高度大于乙种树苗的平均高度,但乙种树苗比甲种树苗长得整齐
C.乙种树苗的平均高度大于甲种树苗的平均高度,且乙种树苗比甲种树苗长得整齐
D.乙种树苗的平均高度大于甲种树苗的平均高度,但甲种树苗比乙种树苗长得整齐
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入![]() ,
,![]() ,则输出的
,则输出的![]() 等于( )
等于( )
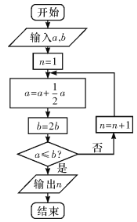
A. 3B. 4C. 5D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com