
分析 先分离出含有a,b的代数式,即$\frac{1}{|a|}$(|a+b|+|a-b|)≥f(x)恒成立,问题转化为求左式的最小值,然后利用绝对值的几何意义得答案.
解答 解:不等式|a+b|+|a-b|≥|a|f(x)对任意a,b∈R恒成立,即$\frac{1}{|a|}$(|a+b|+|a-b|)≥f(x)恒成立,
故f(x)小于等于$\frac{1}{|a|}$(|a+b|+|a-b|)的最小值,
∵$\frac{1}{|a|}$(|a+b|+|a-b|)≥$\frac{1}{|a|}$(|a+b+a-b|)=2,当且仅当(a+b)(a-b)≥0时取等号,
∴$\frac{1}{|a|}$(|a+b|+|a-b|)的最小值等于2.
则|x-1|+|x-2|≤2.
左边的几何意义为数轴上的动点x与两定点1,2的距离和,如图,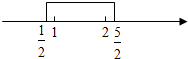
当x∈[$\frac{1}{2},\frac{5}{2}$]时,满足|x-1|+|x-2|≤2.
故x的取值范围是[$\frac{1}{2},\frac{5}{2}$].
点评 本题主要考查了不等式的恒成立问题,通常采用分离参数的方法解决,考查了绝对值的几何意义,属于中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 方程x2-2x+1=0的根构成的集合为{1,1} | |
| B. | {x∈R|x2+1=0}={x∈R|$\left\{\begin{array}{l}{2x+4>0}\\{x+3<0}\end{array}\right.$} | |
| C. | 集合M={(x,y)|x+y=5且2x-y=0}表示的集合是{2,3} | |
| D. | 集合{1,2,3}与集合{3,2,1}是不同的集合 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当x>0且x≠1时,lgx+$\frac{1}{lgx}≥2$ | |
| B. | 当x$∈(0,\frac{π}{2}]$时,sinx+$\frac{4}{sinx}$的最小值为4 | |
| C. | 当x>0时,$\sqrt{x}+\frac{1}{\sqrt{x}}$≥2 | |
| D. | 当0<x≤2时,x-$\frac{1}{x}$无最大值 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com