
【题目】已知数列![]() 和
和![]() 满足:
满足:![]() ,其中
,其中![]() 为实数,
为实数,![]() 为正整数.
为正整数.
(1)对任意实数![]() ,求证:
,求证:![]() 不成等比数列;
不成等比数列;
(2)试判断数列![]() 是否为等比数列,并证明你的结论.
是否为等比数列,并证明你的结论.
【答案】(1)证明见解析;(2)当![]() 时,数列
时,数列![]() 是等比数列.
是等比数列.
【解析】
试题(1)证明否定性命题,可用反证法.如本题中可假设存在![]() ,使
,使![]() 成等比数列,则可由
成等比数列,则可由![]() 来求
来求![]() ,若求不出,说明假设错误,结论是不存在,
,若求不出,说明假设错误,结论是不存在,![]() ,但这个式子化简后为
,但这个式子化简后为![]() ,不可能成立,即
,不可能成立,即![]() 不存在;(2)要判定
不存在;(2)要判定![]() 是等比数列,由题意可先求出
是等比数列,由题意可先求出![]() 的递推关系,
的递推关系,![]() ,这时还不能说明
,这时还不能说明![]() 就是等比数列,还要求出
就是等比数列,还要求出![]() ,
,![]() ,只有当
,只有当![]() 时,数列
时,数列![]() 才是等比数列,因此当
才是等比数列,因此当![]() 时,
时,![]() 不是等比数列,当
不是等比数列,当![]() 时,
时,![]() 是等比数列.
是等比数列.
(1)证明:假设存在一个实数![]() ,使
,使![]() 是等比数列,则有
是等比数列,则有![]() ,
,
即![]() 矛盾.
矛盾.
所以![]() 不成等比数列. 6分
不成等比数列. 6分
(2)因为![]()
![]() 9分
9分
又![]() ,
,
所以当![]() ,
,![]() ,(
,(![]() 为正整数),此时
为正整数),此时![]() 不是等比数列: 11分
不是等比数列: 11分
当![]() 时,
时,![]() ,由上式可知
,由上式可知![]() ,∴
,∴![]() (
(![]() 为正整数) ,
为正整数) ,
故当![]() 时,数列
时,数列![]() 是以
是以![]() 为首项,-
为首项,-![]() 为公比的等比数列. 14分
为公比的等比数列. 14分


科目:高中数学 来源: 题型:
【题目】在某次数学考试中,抽查了1000名学生的成绩,得到频率分布直方图如图所示,规定85分及其以上为优秀.
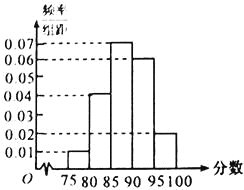
(1)下表是这次抽查成绩的频数分布表,试求正整数![]() 、
、![]() 的值;
的值;
区间 | [75,80) | [80,85) | [85,90) | [90,95) | [95,100] |
人数 | 50 | a | 350 | 300 | b |
(2)现在要用分层抽样的方法从这1000人中抽取40人的成绩进行分析,求抽取成绩为优秀的学生人数;
(3)在根据(2)抽取的40名学生中,要随机选取2名学生参加座谈会,记其中成绩为优秀的人数为X,求X的分布列与数学期望(即均值).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则使按照等差数列的规律计算得出的,下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸
分(1寸![]() 分),已知《易经》中记录的冬至晷影长为130.0寸,夏至晷影长为14.8寸,那么《易经》中所记录的惊蛰的晷影长应为( )
分),已知《易经》中记录的冬至晷影长为130.0寸,夏至晷影长为14.8寸,那么《易经》中所记录的惊蛰的晷影长应为( )
节气 | 冬至 | 小寒(大雪) | 大寒(小雪) | 立春(立冬) | 雨水(霜降) | 惊蛰(寒露) |
晷影(寸) | 135 |
|
|
|
|
|
节气 | 春分(秋分) | 清明(白露) | 谷雨(处暑) | 立夏(立秋) | 小满(大暑) | 芒种(小暑) | 夏至 |
晷影(寸) | 75.5 |
|
|
|
|
| 16.0 |
A.72.4寸B.81.4寸C.82.0寸D.91.6寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考查某种疫苗预防疾病的效果,进行动物实验,得到统计数据如下表:
未发病 | 发病 | 合计 | |
未注射疫苗 | 40 |
|
|
注射疫苗 | 60 |
|
|
合计 | 100 | 100 | 200 |
现从所有试验动物中任取一只,取到“注射疫苗”动物的概率为![]() .
.
(1)求![]() 列联表中的数据
列联表中的数据![]() 的值;
的值;
(2)在图中绘制发病率的条形统计图,并判断疫苗是否有效?
(3)在出错概率不超过![]() 的条件下能否认为疫苗有效?
的条件下能否认为疫苗有效?
附: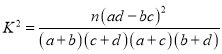 .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,长轴长为4,
,长轴长为4,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,点
的左,右焦点,点![]() 是椭圆
是椭圆![]() 上的任意一点,
上的任意一点,![]() 面积的最大为
面积的最大为![]() ,且取得最大值时
,且取得最大值时![]() 为钝角.
为钝角.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知圆![]() ,点
,点![]() 为圆
为圆![]() 上任意一点,过点
上任意一点,过点![]() 的切线分别交椭圆
的切线分别交椭圆![]() 于
于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的平面展开图如图所示,其中四边形 ABCD 为正方形, E F 分别为PB PC 的中点,在此几何体中,下面结论中一定正确的是( )
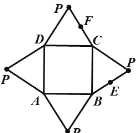
A.直线 AE 与直线 DF 平行B.直线 AE 与直线 DF 异面
C.直线 BF 和平面 PAD 相交D.直线 DF 平面 PBC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com