
【题目】设全集U=R,集合A={x|7﹣6x≤0},集合B={x|y=lg(x+2)},则(UA)∩B等于( )
A.(﹣2, ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.[﹣2, ![]() )
)
D.(﹣2,﹣ ![]() )
)
科目:高中数学 来源: 题型:
【题目】已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)=![]() 是奇函数.
是奇函数.
(1)确定y=f(x)和y=g(x)的解析式;
(2)判断函数f(x)的单调性,并用定义证明;
(3)若对于任意x∈[-5,-1],都有f(1-x)+f(1-2x)>0成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了缓解交通压力,提倡低碳环保,鼓励市民乘坐公共交通系统出行.为了更好地保障市民出行,合理安排运力,有效利用公共交通资源合理调度,在某地铁站点进行试点调研市民对候车时间的等待时间(候车时间不能超过20分钟),以便合理调度减少候车时间,使市民更喜欢选择公共交通.为此在该地铁站的一些乘客中进行调查分析,得到如下统计表和各时间段人数频率分布直方图:
分组 | 等待时间(分钟) | 人数 |
第一组 | [0,5) | 10 |
第二组 | [5,10) | a |
第三组 | [10,15) | 30 |
第四组 | [15,20) | 10 |

(1)求出a的值;要在这些乘客中用分层抽样的方法抽取10人,在这10个人中随机抽取3人至少一人来自第二组的概率;
(2)从这10人中随机抽取3人进行问卷调查,设这3个人共来自X个组,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和
和![]() 的焦点分别为
的焦点分别为![]() ,
, ![]() 交于O,A两点(O为坐标原点),且
交于O,A两点(O为坐标原点),且![]()
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过点O的直线交![]() 的下半部分于点M,交
的下半部分于点M,交![]() 的左半部分于点N,点
的左半部分于点N,点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 为正四棱锥
为正四棱锥![]() 侧棱
侧棱![]() 上异于
上异于![]() ,
, ![]() 的一点,给出下列结论:
的一点,给出下列结论:
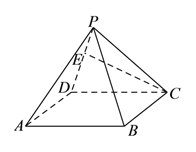
①侧面![]() 可以是正三角形.
可以是正三角形.
②侧面![]() 可以是直角三角形.
可以是直角三角形.
③侧面![]() 上存在直线与
上存在直线与![]() 平行.
平行.
④侧面![]() 上存在直线与
上存在直线与![]() 垂直.
垂直.
其中,所有正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
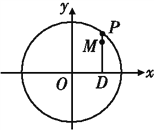
【题目】如图,设P是圆![]() 上的动点,点D是P在x轴上的投影,M为线段PD上一点,且
上的动点,点D是P在x轴上的投影,M为线段PD上一点,且![]() ,
,
(1)当P在圆上运动时,求点M的轨迹C的方程;
(2)求过点(3,0)且斜率为![]() 的直线被轨迹C所截线段的长度.
的直线被轨迹C所截线段的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com