Question

【题目】已知等比数列{an}的前n项和为Sn ， 且 （a∈N+）．
（1）求a的值及数列{an}的通项公式；
（2）设 ，求{bn}的前n项和Tn ．

Answer 1

【答案】解：（1）∵等比数列{an}满足 （a∈N+），

∴当n=1时，6a1=9+a；

当n≥2时， ．

∴ ，

∵n=1时也成立，∴1×6=9+a，解得a=﹣3，

∴ ；

（2） = = ．

当n为奇数时， ；

当n为偶数时，Tn= ．

综上， ．

【解析】（1）先求得n=1的情况，再根据关系式，求得n≥2时{an}的通项公式，最后验证n=1的情况是否满足通项公式；（2）将（1）中求得的{an}的通项公式代入{bn}中，从而求得{bn}的通项公式，求前n项和时分n为奇数与n为偶数的情况进行计算，算的后借助-1的指数幂进行统一表示.
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系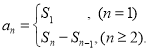；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．