解:(1)根据题意,由x>0,y≥0,-2n(x-3)≥y≥0得0<x≤3,
所以平面区域为Dn内的整点为点(3,0)与在直线x=1和x=2上,
∴直线y=-2n(x-3)与直线x=1和x=2交点纵坐标分别为y1=4n和y2=2n…(6分)
∴Dn内在直线x=1和x=2上的整点个数分别为4n+1和2n+1,
∴an=4n+1+2n+1+1=6n+3 …(7分)
(2)由 b n+1=2bn+an得
bn+1=2bn+6n+3 …(8分)
∴bn+1+6(n+1)+9=2(bn+6n+9)…(9分)
∵b1+6+9=2 …(10分)
∴{bn+6n+9}是以2为首项,公比为2的等比数列…(11分)
∴bn+6n+9=2n …(12分)
∴bn=2n-6n-9.…(13分)
分析:(1)由x>0,y≥0,-2n(x-3)≥y≥0得0<x≤3,所以平面区域为Dn内的整点为点(3,0)与在直线x=1和x=2上,从而可得结论;
(2)由 b n+1=2bn+an得 bn+1+6(n+1)+9=2(bn+6n+9)从而有 {bn+6n+9}是以2为首项,公比为2的等比数列由此可数列{bn+6n+9}的通项,进而可得数列{an}的通项.
点评:本题考查数列的性质和应用,考查二元一次不等式(组)与平面区域,考查学生分析解决问题的能力.

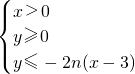 (n∈N*)表示的平面区域为Dn,记Dn内的整点(横坐标和纵坐标均为整数的点)的个数为an.
(n∈N*)表示的平面区域为Dn,记Dn内的整点(横坐标和纵坐标均为整数的点)的个数为an.

 阅读快车系列答案
阅读快车系列答案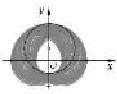 如图,阴影是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}在平面直角坐标系上表示的点集,则阴影中间形如“水滴”部分的面积等于( )
如图,阴影是集合P={(x,y)|(x-cosθ)2+(y-sinθ)2=4,0≤θ≤π}在平面直角坐标系上表示的点集,则阴影中间形如“水滴”部分的面积等于( ) 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组