
【题目】定义在区间[a,b]上的连续函数y=f(x),如果![]() ,使得
,使得![]() ,则称
,则称![]() 为区间[a,b]上的“中值点”,下列函数:
为区间[a,b]上的“中值点”,下列函数:
①![]() ; ②
; ②![]() ; ③
; ③![]() ; ④
; ④![]() 中,在区间[O,1]上“中值点”多于一个的函数序号为( )
中,在区间[O,1]上“中值点”多于一个的函数序号为( )
A. ①② B. ①③ C. ②③ D. ①④
【答案】D
【解析】分析:根据题意,“中值点”的几何意义是在区间![]() 上存在点,使得函数在该点的切线的斜率等于区间
上存在点,使得函数在该点的切线的斜率等于区间![]() 的两个端点连线的斜率值,分别画出四个函数的图像,如图,由此定义再结合函数的图像与性质,对于四个选项逐个加以判断,即得正确答案.
的两个端点连线的斜率值,分别画出四个函数的图像,如图,由此定义再结合函数的图像与性质,对于四个选项逐个加以判断,即得正确答案.
详解:据题意,“中值点”的几何意义是在区间![]() 上存在点,使得函数在该点的切线的斜率等于区间
上存在点,使得函数在该点的切线的斜率等于区间![]() 的两个端点连线的斜率值,如图,
的两个端点连线的斜率值,如图,
对于①,根据题意,在区间![]() 上的任何一点都是“中值点”,故①正确;
上的任何一点都是“中值点”,故①正确;
对于②,根据“中值点”函数的定义,抛物线在区间![]() 只存在一个“中值点”,故②不正确;
只存在一个“中值点”,故②不正确;
对于③,![]() 在区间
在区间![]() 只存在一个“中值点”,故③不正确;
只存在一个“中值点”,故③不正确;
对于④,根据对称性,函数![]() 在区间
在区间![]() 存在两个“中值点”,故④正确,故答案是①④.
存在两个“中值点”,故④正确,故答案是①④.


科目:高中数学 来源: 题型:
【题目】某种树苗栽种时高度为A(A为常数)米,栽种n年后的高度记为f(n).经研究发现f(n)近似地满足 f(n)=![]() ,其中
,其中![]() ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
(1)栽种多少年后,该树木的高度是栽种时高度的8倍;
(2)该树木在栽种后哪一年的增长高度最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1 , 焦点为F2;以F1 , F2为焦点,离心率e=![]() 的椭圆C2与抛物线C1在x轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线C1上一动点,且M在P与Q之间运动.
的椭圆C2与抛物线C1在x轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线C1上一动点,且M在P与Q之间运动.
当m=1时,求椭圆C2的方程;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,底面ABCD是正方形,AC与BD交于点O,
中,底面ABCD是正方形,AC与BD交于点O,![]() 底面ABCD,F为BE的中点,
底面ABCD,F为BE的中点,![]() .
.
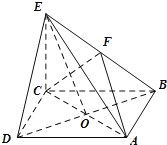
(1)求证:![]() 平面ACF;
平面ACF;
(2)求BE与平面ACE的所成角的正切值;
(3)在线段EO上是否存在点G,使CG![]() 平面BDE ?若存在,求出EG:EO的值,若不存在,请说明理由.
平面BDE ?若存在,求出EG:EO的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cosx(sinx+cosx)﹣![]() .
.
(1)若0<α<![]() , 且sinα=
, 且sinα=![]() , 求f(α)的值;
, 求f(α)的值;
(2)求函数f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为回馈顾客,某商场拟通过摸球兑奖的方式对1000位顾客进行奖励,规定:每位顾客从一个装有4个标有面值的球的袋中一次性随机摸出2个球,球上所标的面值之和为该顾客所获的奖励额.
(1)若袋中所装的4个球中有1个所标的面值为50元,其余3个均为10元,求:
①顾客所获的奖励额为60元的概率;
②顾客所获的奖励额的分布列及数学期望;
(2)商场对奖励总额的预算是60000元,并规定袋中的4个球只能由标有面值10元和50元的两种球组成,或标有面值20元和40元的两种球组成.为了使顾客得到的奖励总额尽可能符合商场的预算且每位顾客所获的奖励额相对均衡,请对袋中的4个球的面值给出一个合适的设计,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,![]() ,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
,第五组,右图是根据试验数据制成的频率分布直方图,已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )
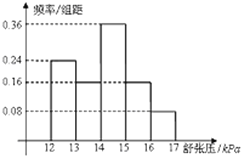
A. 6 B. 8 C. 12 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c∈(0,+∞).
(1)若a=6,b=5,c=4是△ABC边BC,CA,AB的长,证明:cosA∈Q;
(2)若a,b,c分别是△ABC边BC,CA,AB的长,若a,b,c∈Q时,证明:cosA∈Q;
(3)若存在λ∈(-2,2)满足c2=a2+b2+λab,证明:a,b,c可以是一个三角形的三边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,曲线C由上半椭圆C1: ![]() =1(a>b>0,y≥0)和部分抛物线C2:y=﹣x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为
=1(a>b>0,y≥0)和部分抛物线C2:y=﹣x2+1(y≤0)连接而成,C1与C2的公共点为A,B,其中C1的离心率为 ![]() .
. 
(1)求a,b的值;
(2)过点B的直线l与C1 , C2分别交于点P,Q(均异于点A,B),若AP⊥AQ,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com