
【题目】等差数列{an}中,已知an>0,a1+a2+a3=15,且a1+2,a2+5,a3+13构成等比数列{bn}的前三项.
(1)求数列{an},{bn}的通项公式;
(2)求数列{anbn}的前n项和Tn .
【答案】
(1)解:设设等差数列的公差为d,则由已知得:a1+a2+a3=3a2=15,即a2=5,
又(5﹣d+2)(5+d+13)=100,解得d=2或d=﹣13(舍),
a1=a2﹣d=3,
∴an=a1+(n﹣1)×d=2n+1,
又b1=a1+2=5,b2=a2+5=10,
∴q=2
∴ ![]()
(2)解:∵ ![]() ,
,
![]() ,
,
两式相减得 ![]() ,
,
则 ![]()
【解析】(1)利用等差数列的通项公式及其性质可得an . 再利用等比数列的通项公式即可得出bn . (2)利用“错位相减法”与等比数列的前n项和公式即可得出.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系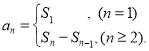 ,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
,以及对数列的通项公式的理解,了解如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,M,N,P分别是B1B,B1C1 , CD的中点,则MN与D1P所成角的余弦值为( ) 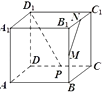
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(Rt△FHE,H是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米, ![]() 米,记∠BHE=θ.
米,记∠BHE=θ. 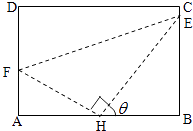
(1)试将污水净化管道的长度L表示为θ的函数,并写出定义域;
(2)若 ![]() ,求此时管道的长度L;
,求此时管道的长度L;
(3)当θ取何值时,污水净化效果最好?并求出此时管道的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)将曲线![]() 的极坐标方程化为直坐标方程,并说明曲线
的极坐标方程化为直坐标方程,并说明曲线![]() 的形状;
的形状;
(2)若直线![]() 经过点
经过点![]() ,求直线
,求直线![]() 被曲线
被曲线![]() 截得的线段
截得的线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}满足 ![]() =1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
=1,公差d∈(﹣1,0),当且仅当n=9时,数列{an}的前n项和Sn取得最大值,求该数列首项a1的取值范围( )
A.( ![]() ,
, ![]() )
)
B.[ ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() )
)
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com