已知等比数列
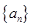
的各项均为正数,且
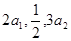
成等差数列,
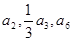
成等比数列.
(1)求数列
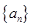
的通项公式;
(2)已知
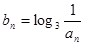
,记
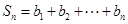
,
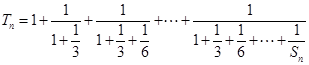
,求证:
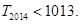
(1)
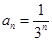
;(2)参考解析
试题分析:(1)又等比数列
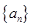
的各项均为正数,且
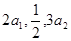
成等差数列,
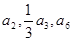
成等比数列.
可得到两个等式,解方程组可得结论.
(2)由(1)可得数列
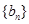
的通项,即可计算
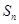
,由于
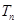
是一个复合的形式,所以先计算通项式
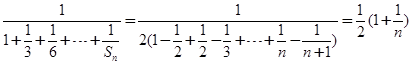
.即可得到
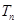
.又由于
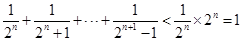
.即可得到结论.
试题解析:设等比数列
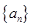
的公比为
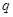
,依题意可得
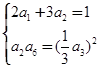
解得
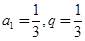
.所以通项
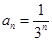
.
(2)由(1)得
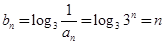
.所以

.由
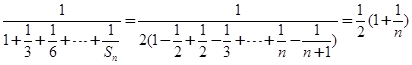
.所以
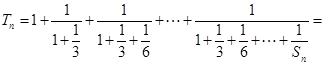
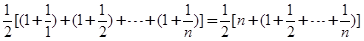
.所以
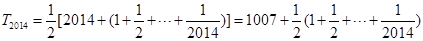
即等价于证明
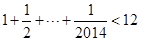
.

.所以
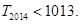
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
在数列{
an}中,
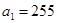
,
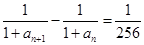
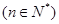
,
(1)求数列
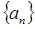
的通项公式
(2)设
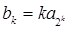
(
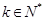
),记数列
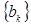
的前k项和为
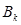
,求
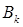
的最大值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知数列
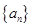
中,
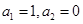
其前
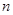
项和
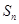
满足:


(1)试求数列
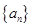
的通项公式;
(2)求数列
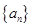
的前
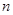
项和
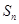
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知
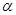
为锐角,且
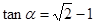
,函数
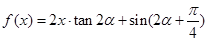
,数列
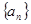
的首项
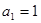
,
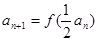
.
(1)求函数

的表达式;(2)求数列
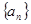
的前
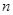
项和

.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知{a
n}是等差数列,a
1=1,公差d≠0,Sn为其前
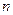
项和,若a
1,a
2,a
5成等比数列,则S
8="(" )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
用数学归纳法证明

,在验证n=1成立时,等式左边是
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知数列{a
n}的通项公式
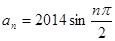
,则
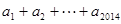
=( )
查看答案和解析>>

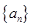 的各项均为正数,且
的各项均为正数,且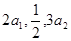 成等差数列,
成等差数列,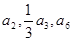 成等比数列.
成等比数列.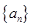 的通项公式;
的通项公式;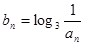 ,记
,记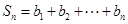 ,
,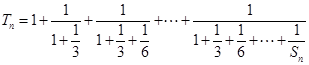 ,求证:
,求证: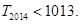
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 项和,若a1,a2,a5成等比数列,则S8="(" )
项和,若a1,a2,a5成等比数列,则S8="(" )