分析:(Ⅰ)连接A1D,根据题意可知A1D是B1D在平面A1ADD1上的射影,从而得到∠A1DB1是直线B1D和平面A1ADD1所成的角,
在Rt△B1A1D中,求出此角即可;
(Ⅱ)根据比例关系可知△A1AD~△ADE,从而得到∠A1DA=∠AED,根据角与角的关系可知A1D⊥AE,而A1D是B1D在平面A1ADD1上的射影,最后根据三垂线定理得结论;
(Ⅲ)设A1D∩AE=F,连接CF,根据二面角的平面角的定义可知∠DFC是二面角C-AE-D的平面角,在Rt△ADE中,求出DF,在Rt△FDC中,求出角DFC,从而求出二面角C-AE-D的大小.
解答:解:
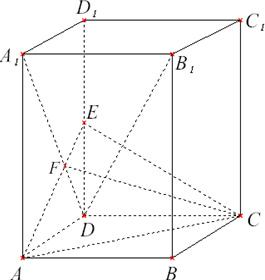
(Ⅰ)连接A
1D.∵ABCD-A
1B
1C
1D
1是正四棱柱,
∴A
1B
1⊥平面A
1ADD
1,
∴A
1D是B
1D在平面A
1ADD
1上的射影,
∴∠A
1DB
1是直线B
1D和平面A
1ADD
1所成的角(2分)
在Rt△B
1A
1D中,
tanA1DB1==,
∴∠A
1DB
1=30°,
即直线B
1D和平面A
1ADD
1所成角的大小是30°(4分)
(Ⅱ)证明:在Rt△A
1AD和Rt△ADE中,
∵
==,
∴△A
1AD~△ADE,∴∠A
1DA=∠AED.
∴∠A
1DA+∠EAD=∠AED+∠EAD=90°,
∴A
1D⊥AE(7分)
由(Ⅰ)知,A
1D是B
1D在平面A
1ADD
1上的射影,
根据三垂线定理得,B
1D⊥AE(9分)
(Ⅲ)设A
1D∩AE=F,连接CF.∵CD⊥平面A
1ADD
1,且AE⊥DF,
根据三垂线定理得,AE⊥CF,∴∠DFC是二面角C-AE-D的平面角(11分)
在Rt△ADE中,由
AD•DE=AE•DF?DF==.
在Rt△FDC中,
tanDFC==,∴∠DFC=60°,
即二面角C-AE-D的大小是60°(14分)
点评:本题主要考查了线面所成角,以及三垂线定理和二面角的度量,同时考查了空间想象能力,计算能力和转化与划归的思想,属于中档题.

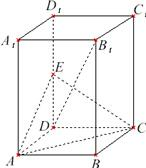 如图,在正四棱柱ABCD-A1B1C1D1中,AA1=
如图,在正四棱柱ABCD-A1B1C1D1中,AA1= (Ⅰ)连接A1D.∵ABCD-A1B1C1D1是正四棱柱,
(Ⅰ)连接A1D.∵ABCD-A1B1C1D1是正四棱柱,

 智慧小复习系列答案
智慧小复习系列答案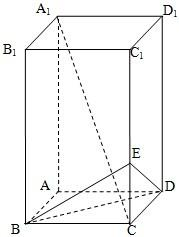 如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点.
如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点.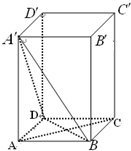 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=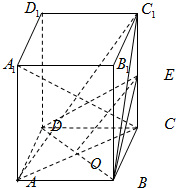 (2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=
(2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=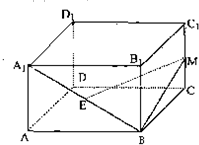 如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点. (2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )
(2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )