
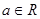 ,讨论函数
,讨论函数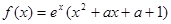 的极值点的个数
的极值点的个数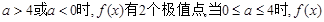 无极值点
无极值点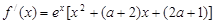 令
令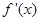 =0得
=0得 .
.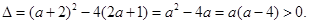 即
即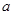 <0或
<0或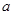 >4时
>4时 有两个不同的实根
有两个不同的实根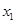 ,
,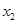 ,
,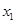 <
<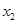 ,则
,则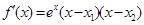 ,
,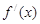 在
在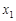 和
和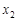 两侧的符号都相反,即此时
两侧的符号都相反,即此时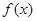 有两个极值点.
有两个极值点.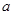 =0或
=0或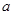 =4时,方程
=4时,方程 有两个相同的实根
有两个相同的实根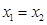 ,于是
,于是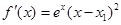 ,故在
,故在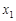 的两侧均有
的两侧均有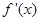 >0,因此
>0,因此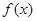 无极值.
无极值.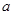 <4时
<4时 无实数根,
无实数根,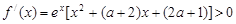 ,
,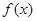 为增函数,此时
为增函数,此时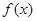 无极值.
无极值.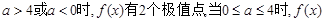 无极值点.
无极值点.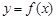 在某个区间内可导,函数
在某个区间内可导,函数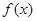 在某点取得极值的充要条件是该点的导数为零且在该点两侧的导数值异号.本题从逆向思维的角度出发,根据题设结构进行逆向联想,合理地实现了问题的转化,使抽象的问题具体化
在某点取得极值的充要条件是该点的导数为零且在该点两侧的导数值异号.本题从逆向思维的角度出发,根据题设结构进行逆向联想,合理地实现了问题的转化,使抽象的问题具体化

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com