选修4-5:不等式选讲
(Ⅰ)解不等式:|2x-1|-|x|<1;
(Ⅱ)设f(x)=x2-x+1,实数a满足|x-a|<1,求证:|f(x)-f(a)|<2(|a|+1).
解:(Ⅰ)当x<0时,原不等式可化为-2x+x<0,解得x>0,又∵x<0,∴x不存在.
当
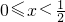
时,原不等式可化为-2x-x<0,解得x>0,又∵
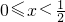
,∴

.
当

时,原不等式可化为2x-1-x<1,解得x<2,又∵

,∴
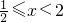
.
综上,原不等式的解集为{x|0<x<2}.
(Ⅱ)∵f(x)=x
2-x+1,实数a满足|x-a|<1,
故|f(x)-f(a)|=|x
2-x-a
2+a|=|x-a|•|x+a-1|<|x+a-1|=|x-a+2a-1|≤|x-a|+|2a-1|<1+|2a|+1=2(|a|+1).
∴|f(x)-f(a)|<2(|a|+1).
分析:(Ⅰ)分x<0、
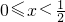
、

三种情况,分别去掉绝对值,求出不等式的解集,再取并集,即得所求.
(Ⅱ)根据|f(x)-f(a)|=|x
2-x-a
2+a|=|x-a|•|x+a-1|<|x+a-1|=|x-a+2a-1|≤|x-a|+|2a-1|<1+|2a|+1,证得结果.
点评:本题主要考查绝对值不等式的解法,绝对值不等式的性质,用放缩法证明不等式,体现了分类讨论的数学思想,属于中档题.

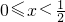 时,原不等式可化为-2x-x<0,解得x>0,又∵
时,原不等式可化为-2x-x<0,解得x>0,又∵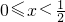 ,∴
,∴ .
. 时,原不等式可化为2x-1-x<1,解得x<2,又∵
时,原不等式可化为2x-1-x<1,解得x<2,又∵ ,∴
,∴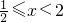 .
.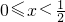 、
、 三种情况,分别去掉绝对值,求出不等式的解集,再取并集,即得所求.
三种情况,分别去掉绝对值,求出不等式的解集,再取并集,即得所求.
