
【题目】设函数![]() ,实数
,实数![]()
![]() 满足
满足![]() ,若
,若![]() ,则实数
,则实数![]() ________,
________,![]() ________.
________.
【答案】![]()
![]()
【解析】
根据题目给出的等式f(a)=f(![]() ),代入函数解析式得到a、b的关系,从而判断出f(10a+6b+21)的符号,再把f(10a+6b+21)=4lg2,转化为含有一个字母的式子即可求解.
),代入函数解析式得到a、b的关系,从而判断出f(10a+6b+21)的符号,再把f(10a+6b+21)=4lg2,转化为含有一个字母的式子即可求解.
因为f(a)=f(![]() ),所以|lg(a+1)|=|lg(
),所以|lg(a+1)|=|lg(![]() 1)|=|lg(
1)|=|lg(![]() )|=|lg(b+2)|,
)|=|lg(b+2)|,
所以a+1=b+2,或(a+1)(b+2)=1,又因为a<b,所以a+1≠b+2,所以(a+1)(b+2)=1.
又由f(a)=|lg(a+1)|有意义知a+1>0,从而0<a+1<b+1<b+2,
于是0<a+1<1<b+2.
所以(10a+6b+21)+1=10(a+1)+6(b+2)=6(b+2)![]() 1.
1.
从而f(10a+6b+21)=|lg[6(b+2)![]() ]|=lg[6(b+2)
]|=lg[6(b+2)![]() ].
].
又f(10a+6b+21)=4lg2,
所以lg[6(b+2)![]() ]=4lg2,
]=4lg2,
故6(b+2)![]() 16.解得b
16.解得b![]() 或b=﹣1(舍去).
或b=﹣1(舍去).
把b![]() 代入(a+1)(b+2)=1解得a
代入(a+1)(b+2)=1解得a![]() .
.
所以 a![]() ,b
,b![]() .
.
故答案为:![]() ;
;![]() ..
..


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() .
.
(1)若圆![]() 与
与![]() 轴的正半轴相切,且该圆截
轴的正半轴相切,且该圆截![]() 轴所得弦的长为
轴所得弦的长为![]() ,求圆
,求圆![]() 的标准方程;
的标准方程;
(2)在(1)的条件下,直线![]() 与圆
与圆![]() 交于两点
交于两点![]() ,
,![]() ,若以
,若以![]() 为直径的圆过坐标原点
为直径的圆过坐标原点![]() ,求实数
,求实数![]() 的值;
的值;
(3)已知点![]() ,圆
,圆![]() 的半径为3,且圆心
的半径为3,且圆心![]() 在第一象限,若圆
在第一象限,若圆![]() 上存在点
上存在点![]() ,使
,使![]() (
(![]() 为坐标原点),求圆心
为坐标原点),求圆心![]() 的纵坐标的取值范围.
的纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高三复习效果,从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩,分成6组制成频率分布直方图如图所示:
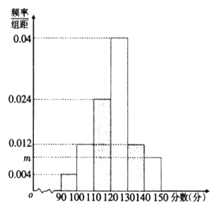
(1)求![]() 的值;并且计算这50名同学数学成绩的样本平均数
的值;并且计算这50名同学数学成绩的样本平均数![]() ;
;
(2)该学校为制定下阶段的复习计划,从成绩在![]() 的同学中选出3位作为代表进行座谈,记成绩在
的同学中选出3位作为代表进行座谈,记成绩在![]() 的同学人数位
的同学人数位![]() ,写出
,写出![]() 的分布列,并求出期望.
的分布列,并求出期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①线性相关系数![]() 越大,两个变量的线性相关性越强;反之,线性相关性越弱;
越大,两个变量的线性相关性越强;反之,线性相关性越弱;
②由变量![]() 和
和![]() 的数据得到其回归直线方程
的数据得到其回归直线方程![]() ,则
,则![]() 一定经过点
一定经过点![]() ;
;
③从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;
④将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
⑤在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.1个单位,
平均增加0.1个单位,
其中真命题的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口的水深![]() (米)是时间
(米)是时间![]() (
(![]() ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过长期观测,![]() 可近似的看成是函数
可近似的看成是函数![]()
(1)根据以上数据,求出![]() 的解析式;
的解析式;
(2)若船舶航行时,水深至少要![]() 米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司每天从甲地运货物到乙地,统计最近的200次可配送的货物量,可得可配送的货物量的频率分布直方图,所图所示,回答以下问题(直方图中每个小组取中间值作为该组数据的替代值).
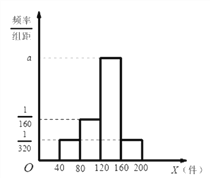
(1)求该物流公司每天从甲地到乙地平均可配送的货物量;
(2)该物流公司拟购置货车专门运营从甲地到乙地的货物,一辆货车每天只能运营一趟,每辆车每趟最多只能装载40件货物,满载发车,否则不发车.若发车,则每辆车每趟可获利1000元;若未发车,则每辆车每天平均亏损200元.为使该物流公司此项业务的营业利润最大,该物流公司应该购置几辆货车?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com