Question

【题目】已知Sn为等比数列{an}的前n项和且S4=S3+3a3 ， a2=9．
（1）求数列{an}的通项公式
（2）设bn=（2n﹣1）an ， 求数列{bn}的前n项和Tn ．

Answer 1

【答案】
（1）解：设等比数列{an}的公比为q，

S4=S3+3a3，a2=9，可得

a4=S4﹣S3=3a3，即q= =3，

a1q=9，可得a1=3，

则数列{an}的通项公式为an=a1qn﹣1=3n；

（2）解：bn=（2n﹣1）an=（2n﹣1）3n；

则前n项和Tn=131+332+…+（2n﹣1）3n；

3Tn=132+333+…+（2n﹣1）3n+1；

两式相减可得，﹣2Tn=3+2（32+33+…+3n）﹣（2n﹣1）3n+1

=3+2 ﹣（2n﹣1）3n+1；

化简可得Tn=3+（n﹣1）3n+1．

【解析】（1）设等比数列{an}的公比为q，运用等比数列的通项公式可得首项和公比，即可得到所求通项公式；（2）求得bn=（2n﹣1）an=（2n﹣1）3n；运用数列的求和方法：错位相减法，结合等比数列的求和公式，化简整理即可得到所求和．
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系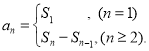；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．