
如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.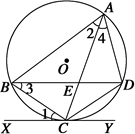
(1)求证:△ABE≌△ACD;
(2)若AB=6 cm,BC=4 cm,求AE的长.
(1)见解析;(2)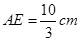 .
.
解析试题分析:(1)欲证三角形全等,需牢牢掌握 这种证明方法和所需要的条件.本小题
这种证明方法和所需要的条件.本小题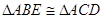 ,
, (已知),下寻找另外的边和角,考虑到这里有圆,所以运用同弧所对应的圆周角相等可得
(已知),下寻找另外的边和角,考虑到这里有圆,所以运用同弧所对应的圆周角相等可得 (弧
(弧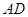 所对),接着证明
所对),接着证明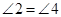 (其他角和边不好证,同时这里有弦切角可以利用)
(其他角和边不好证,同时这里有弦切角可以利用)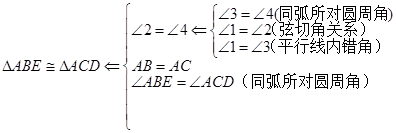 .(2)欲求
.(2)欲求 ,因
,因 ,则可转化为求
,则可转化为求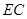 ,考虑到
,考虑到 ,需将
,需将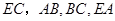 联系起来就得考虑三角形相似.注意到
联系起来就得考虑三角形相似.注意到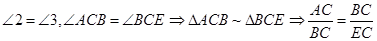 ,
,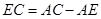 .
.
试题解析:(1)证明 因为XY是⊙O的切线,所以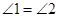 .
.
因为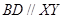 ,所以
,所以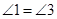 ,∴
,∴ . 2分
. 2分
因为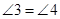 ,所以
,所以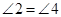 . 4分
. 4分
因为 ,又因为
,又因为 ,
,
所以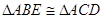 . 5分
. 5分
(2)解 因为 ,
,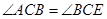 ,
,
所以 , 7分
, 7分
所以 , 即
, 即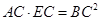 8分
8分
因为 ,
, ,
,
所以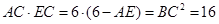 .所以
.所以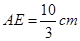 . 10分
. 10分
考点:(1)三角形全等的证明;(2)三角形相似的证明与应用;(3)圆性质的应用.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:解答题
如图,圆O的直径AB= 10,P是AB延长线上一点,BP=2,割线PCD交圆O于点C、D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
(Ⅰ)求证: PEC=
PEC=  PDF
PDF
(Ⅱ)求PE PF的值
PF的值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,△ABC中,AB=AC,∠BAC=90°,AE= AC,BD=
AC,BD= AB,点F在BC上,且CF=
AB,点F在BC上,且CF= BC.求证:
BC.求证:
(1)EF⊥BC;
(2)∠ADE=∠EBC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分10分)选修4-1:几何证明选讲
如图,四边形 是
是 的内接四边形,
的内接四边形, 的延长线与
的延长线与 的延长线交于点
的延长线交于点 ,且
,且 .
.
(Ⅰ)证明: ;
;
(Ⅱ)设 不是
不是 的直径,
的直径, 的中点为
的中点为 ,且
,且 ,证明:
,证明: 为等边三角形.
为等边三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连结AE,BE.证明:
(1)∠FEB=∠CEB;
(2)EF2=AD·BC.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=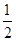 CD.
CD.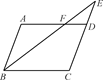
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求平行四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com