
【题目】直四棱柱![]() 被平面
被平面![]() 所截,所得的一部分如图所示,
所截,所得的一部分如图所示,![]() .
.
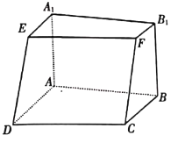
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,平面
,平面![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)要证线面平行只要证平面外一条直线平行于平面内一条直线即可,本题证明![]() 为平行四边形即可得证;
为平行四边形即可得证;
(2)根据所给关系,建立直角坐标系,求出两平面的法向量,利用平面![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,可求出E点坐标,再利用几何关系或者投影即可得解.
,可求出E点坐标,再利用几何关系或者投影即可得解.
(1)依题:平面![]() 与两平行平面
与两平行平面![]() ,
,![]() 的交线分别为
的交线分别为![]() ,
,![]() ,
,
故有![]() ,又
,又![]() ,故有平行四边形
,故有平行四边形![]() ,
,
∴![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)![]() 中,由余弦定理可得
中,由余弦定理可得![]() ,由勾股定理得
,由勾股定理得![]() ,又
,又![]() 平面
平面![]() ,
,
故而![]() ,
,![]() ,
,![]() 两两垂直,如图建系.
两两垂直,如图建系.
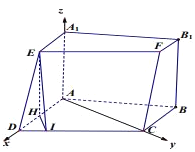
【法一求![]() 】取
】取![]() 中点
中点![]() ,由
,由![]() ,
,![]() 得平行四边形
得平行四边形![]() ,
,
∴![]() ,
,![]() 平面
平面![]() ,作
,作![]() ,(连
,(连![]() ),又
),又![]() ,
,
∴![]() 平面
平面![]() ,得
,得![]() ,又
,又![]() ,∴
,∴![]() 为所求二面角的平面角.
为所求二面角的平面角.
易求![]() ,又
,又![]() ,
,![]() .
.
【法二求![]() 】面
】面![]() 的法向量显然为
的法向量显然为![]() ,设面
,设面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,
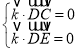 ,令
,令![]() ,
,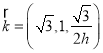 ,依题:
,依题: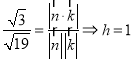 .
.
由![]() 平面
平面![]() ,点
,点![]() 到平面
到平面![]() 的距离转化为
的距离转化为![]() 到平面
到平面![]() 的距离
的距离![]() ,
,![]() ,
,![]() ,
,
![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,
,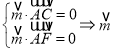 可为
可为![]() ,
,
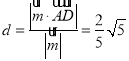 .
.


科目:高中数学 来源: 题型:
【题目】槟榔原产于马来西亚,中国主要分布在云南、海南及台湾等热带地区,亚洲热带地区广泛栽培.槟榔是重要的中药材,南方一些少数民族还有将果实作为一种咀嚼嗜好品,但其被世界卫生组织国际癌症研究机构列为致癌物清单Ⅰ类致癌物.云南某民族中学为了解![]() ,
,![]() 两个少数民族班的学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名学生进行调查,经他们平均每周咀嚼槟榔的颗数作为样本,绘制成如图所示的茎叶图(图中的茎表示十位数字,叶表示个位数字).
两个少数民族班的学生咀嚼槟榔的情况,分别从这两个班中随机抽取5名学生进行调查,经他们平均每周咀嚼槟榔的颗数作为样本,绘制成如图所示的茎叶图(图中的茎表示十位数字,叶表示个位数字).

(1)你能否估计哪个班的学生平均每周咀嚼槟榔的颗数较多?
(2)在被抽取的10名学生中,从平均每周咀嚼槟榔的颗数不低于20颗的学生中随机抽取3名学生,求抽到![]() 班学生人数
班学生人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,AB=1,AD=2,△ABD沿对角线BD翻折,形成三棱锥A﹣BCD.
①当![]() 时,三棱锥A﹣BCD的体积为
时,三棱锥A﹣BCD的体积为![]() ;
;
②当面ABD⊥面BCD时,AB⊥CD;
③三棱锥A﹣BCD外接球的表面积为定值.
以上命题正确的是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 垂直平分线上的一点,且
垂直平分线上的一点,且![]() ,固定边
,固定边![]() ,在平面
,在平面![]() 内移动顶点
内移动顶点![]() ,使得
,使得![]() 的内切圆始终与
的内切圆始终与![]() 切于线段
切于线段![]() 的中点,且
的中点,且![]() 、
、![]() 在直线
在直线![]() 的同侧,在移动过程中,当
的同侧,在移动过程中,当![]() 取得最小值时,
取得最小值时,![]() 的面积为( )
的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年反映社会现实的电影《我不是药神》引起了很大的轰动,治疗特种病的创新药研发成了当务之急.为此,某药企加大了研发投入,市场上治疗一类慢性病的特效药品![]() 的研发费用
的研发费用![]() (百万元)和销量
(百万元)和销量![]() (万盒)的统计数据如下:
(万盒)的统计数据如下:
研发费用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
销量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
(1)根据数据用最小二乘法求出![]() 与
与![]() 的线性回归方程
的线性回归方程![]() (系数用分数表示,不能用小数);
(系数用分数表示,不能用小数);
(2)该药企准备生产药品![]() 的三类不同的剂型
的三类不同的剂型![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() ,第二次检测时,三类剂型
,第二次检测时,三类剂型![]() ,
,![]() ,
,![]() 合格的概率分别为
合格的概率分别为![]() ,
,![]() ,
,![]() .两次检测过程相互独立,设经过两次检测后
.两次检测过程相互独立,设经过两次检测后![]() ,
,![]() ,
,![]() 三类剂型合格的种类数为
三类剂型合格的种类数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:(1)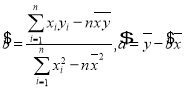 (2)
(2)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() (侧棱垂直于底面,且底面三角形
(侧棱垂直于底面,且底面三角形![]() 是等边三角形)中,
是等边三角形)中,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
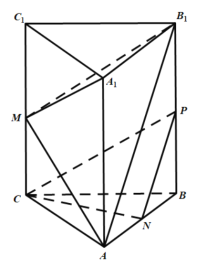
(1)求证:平面![]() ∥平面
∥平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() 使
使![]() 平面
平面![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,也请说明理由.
的位置;若不存在,也请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 存在极值,求实数a的取值范围;
存在极值,求实数a的取值范围;
(2)设![]() ,设
,设![]() 是定义在
是定义在![]() 上的函数.
上的函数.
(ⅰ)证明:![]() 在
在![]() 上为单调递增函数(
上为单调递增函数(![]() 是
是![]() 的导函数);
的导函数);
(ⅱ)讨论![]() 的零点个数.
的零点个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com