
【题目】已知函数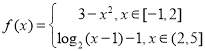 .
.
(1)在直角坐标系内直接画出![]() 的图象;
的图象;
(2)写出![]() 的单调区间,并指出单调性(不要求证明);
的单调区间,并指出单调性(不要求证明);
(3)若函数![]() 有两个不同的零点,求实数
有两个不同的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)图见解析;(2)在[﹣1,0]上单调递增,在[0,2]上单调递减,在[2,5]上单调递增;(3)(﹣1,1]∪[2,3)
【解析】
(1)直接画出图像得到答案.
(2)根据图像得到函数的单调区间.
(3)变换得到![]() ,讨论
,讨论![]() 的不同取值得到答案.
的不同取值得到答案.
(1)由题意,函数f(x)大致图像如下:
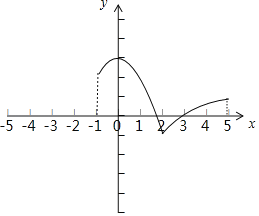
(2)根据(1)中函数f(x)大致图像:
函数f(x)在[﹣1,0]上单调递增,在[0,2]上单调递减,在[2,5]上单调递增.
(3)根据(1)中函数f(x)大致图象,可知
①当t<﹣1时,直线y=t与y=f(x)没有交点;
②当t=﹣1时,直线y=t与y=f(x)有1个交点;
③当﹣1<t≤1时,直线y=t与y=f(x)有2个交点;
④当1<t<2时,直线y=t与y=f(x)有1个交点;
⑤当2≤t<3时,直线y=t与y=f(x)有2个交点;
⑥当t=3时,直线y=t与y=f(x)有1个交点;
⑦当t>3时,直线y=t与y=f(x)没有交点.
∴若函数y=t﹣f(x)有两个不同的零点,实数t的取值范围为:(﹣1,1]∪[2,3).


科目:高中数学 来源: 题型:
【题目】现有甲乙两组学生,分别参加某项体能测试,所得成绩的茎叶图如图.规定测试成绩大于等于90分为优秀,80至89分为良好,60至79分为合格,60分以下为不合格.
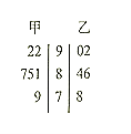
(1)现从甲组数据中抽取一名学生的成绩,有放回地抽取6次,记抽到优秀成绩的次数为X,求![]() ;
;
(2)从甲、乙两组学生中任取3名学生,记抽中成绩优秀的学生数为Y,求Y的概率分布与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 中有:①若
中有:①若![]() ,则
,则![]() ;②若
;②若![]() ,则
,则![]() —定为等腰三角形;③若
—定为等腰三角形;③若![]() ,则
,则![]() —定为直角三角形;④若
—定为直角三角形;④若![]() ,且该三角形有两解,则
,且该三角形有两解,则![]() 的范围是
的范围是![]() .以上结论中正确的个数有( )
.以上结论中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的“十八大”之后,做好农业农村工作具有特殊重要的意义.国家为了更 好地服务于农民、开展社会主义新农村工作,派调查组到农村某地区考察.该地区有100户农 民,且都从事蔬菜种植.据了解,平均每户的年收入为6万元.为了调整产业结构,当地政府决 定动员部分农民从事蔬菜加工.据统计,若动员![]() 户农民从事蔬菜加工,则剩下的继续 从事蔬菜种植的农民平均每户的年收入有望提高
户农民从事蔬菜加工,则剩下的继续 从事蔬菜种植的农民平均每户的年收入有望提高![]() ,而从事蔬菜加工的农民平均每户的年收入为
,而从事蔬菜加工的农民平均每户的年收入为![]() 万元.
万元.
(1)在动员![]() 户农民从事蔬菜加工后,要使剩下
户农民从事蔬菜加工后,要使剩下![]() 户从事蔬菜种植的所有农民总年收 入不低于动员前100户从事蔬菜种植的所有农民年总年收入,求
户从事蔬菜种植的所有农民总年收 入不低于动员前100户从事蔬菜种植的所有农民年总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这![]() 户农民从事蔬菜加工的总年收入始终不高于
户农民从事蔬菜加工的总年收入始终不高于![]() 户从事蔬菜种植的所有农民年总年收入,求
户从事蔬菜种植的所有农民年总年收入,求![]() 的最大值.(参考数据:
的最大值.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]()
![]()
![]() ,若
,若![]() ,且
,且![]() 的图象相邻的对称轴间的距离不小于
的图象相邻的对称轴间的距离不小于![]() .
.
(1)求![]() 的取值范围.
的取值范围.
(2)若当![]() 取最大值时,
取最大值时, ![]() ,且在
,且在![]() 中,
中, ![]() 分别是角
分别是角![]() 的对边,其面积
的对边,其面积![]() ,求
,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数![]() .
.
(1)若x=2是函数f(x)的极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)在![]() 上为单调增函数,求a的取值范围;
上为单调增函数,求a的取值范围;
(3)设m,n为正实数,且m>n,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com