
分析 ①先将f(0)>0,f(1)>0,利用函数式中的a,b,c进行表示,再结合等式关系利用不等式的基本性质即可得到a和$\frac{a}{b}$的范围即可.
②欲证明方程f(x)=0在(0,1)内有两个实根,根据根的存在性定理,只须证明某一个函数值小于0即可,最后只须证明在二次函数顶点处的函数值小于0即可.
解答 证明:①因为f(0)>0,f(1)>0,
所以c>0,3a+2b+c>0.
由条件a+b+c=0,消去b,得a>c>0;
由条件a+b+c=0,消去c,得a+b<0,2a+b>0.
故-2<$\frac{a}{b}$<-1;
②抛物线f(x)=3ax2+2bx+c的顶点坐标为(-$\frac{b}{3a}$,$\frac{3ac-{b}^{2}}{3a}$),
在-2<$\frac{a}{b}$<-1的两边乘以-$\frac{1}{3}$,得$\frac{1}{3}$<-$\frac{b}{3a}$<$\frac{2}{3}$.
又因为f(0)>0,f(1)>0,
而f(-$\frac{b}{3a}$)=-$\frac{{a}^{2}+{c}^{2}-ac}{3a}$<0,
所以方程f(x)=0在区间(0,-$\frac{b}{3a}$)与(-$\frac{b}{3a}$,1)内分别有一实根.
故方程f(x)=0在(0,1)内有两个实根.
点评 本题主要考查二次函数的基本性质与不等式的应用等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.


科目:高中数学 来源: 题型:解答题
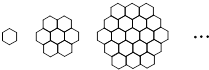 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看做是一各正六边形,如图为一组蜂巢的截面图,其中第一图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n个图的蜂巢总数.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看做是一各正六边形,如图为一组蜂巢的截面图,其中第一图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n个图的蜂巢总数.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (-∞,2] | C. | (2,+∞) | D. | [2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
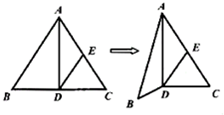 如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )
如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com