

 少年后,开始盈利?
少年后,开始盈利? 引进该设备若干年后,有两种处理方案:
引进该设备若干年后,有两种处理方案:科目:高中数学 来源:不详 题型:解答题
 第一象限部分上的一系列点
第一象限部分上的一系列点 与y正半轴上的点
与y正半轴上的点 及原点,构成一系列正三角形
及原点,构成一系列正三角形 (记
(记 为O),记
为O),记 。
。 的值;(2)求数列
的值;(2)求数列 的通项公式
的通项公式 ;
;

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 前
前 项和为
项和为 ,且
,且 。其中
。其中 为实常数,
为实常数, 且
且 。
。 是等比数列;
是等比数列; 的公比满足
的公比满足 且
且 ,求
,求 的
的 时,设
时,设 ,是否存在最大的正整数
,是否存在最大的正整数 ,使得对任意
,使得对任意 均有
均有 成立,若存在求出
成立,若存在求出 的值,若不存在请说明理由。
的值,若不存在请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 证明以下命题:
证明以下命题: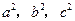 成等差数列。
成等差数列。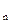 ,其边长
,其边长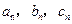 为正整数且
为正整数且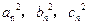 成等差数列。
成等差数列。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 条的为第
条的为第 层,每一层的竖直通道从左到右分别称为第1通道、第2通道,……,现在有一个小球从入口向下(只能向下,不能向上)运动,小球在每个交点处向左到达下一层或者向右到达下一层的可能性是相同的。小球到达第
层,每一层的竖直通道从左到右分别称为第1通道、第2通道,……,现在有一个小球从入口向下(只能向下,不能向上)运动,小球在每个交点处向左到达下一层或者向右到达下一层的可能性是相同的。小球到达第 层第
层第 通道的不同路径数称为
通道的不同路径数称为 ,如小球到达第二层第1通道和第二层第2通道的路径都只有一种情况,因此,
,如小球到达第二层第1通道和第二层第2通道的路径都只有一种情况,因此, ,
, 。
。
 ,
, ,
, ;
; ,以及小球到达第5层第2通道的概率;
,以及小球到达第5层第2通道的概率;
 ,并证明;
,并证明;
 (不用证明)。
(不用证明)。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com