
【题目】已知动点![]() 到定点
到定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比值为常数
的距离的比值为常数![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() ,
, ![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]()
![]() ,且
,且![]() ,求以
,求以![]() ,
, ![]() ,
, ![]() ,
, ![]() 为顶点的凸四边形的面积
为顶点的凸四边形的面积![]() 的最大值.
的最大值.
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:
【题目】已知两个不相等的非零向量 ![]() ,
, ![]() ,两组向量
,两组向量 ![]() 和
和 ![]() 均由2个
均由2个 ![]() 和3个
和3个 ![]() 排列而成,记S=
排列而成,记S= ![]() ,Smin表示S所有可能取值中的最小值,则下列命题中
,Smin表示S所有可能取值中的最小值,则下列命题中
1)S有5个不同的值;(2)若 ![]() ⊥
⊥ ![]() 则Smin与|
则Smin与| ![]() |无关;(3)若
|无关;(3)若 ![]() ∥
∥ ![]() 则Smin与|
则Smin与| ![]() |无关;(4)若|
|无关;(4)若| ![]() |>4|
|>4| ![]() |,则Smin>0;(5)若|
|,则Smin>0;(5)若| ![]() |=2|
|=2| ![]() |,Smin=8|
|,Smin=8| ![]() |2 , 则
|2 , 则 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() .正确的是( )
.正确的是( )
A.(1)(2)
B.(2)(4)
C.(3)(5)
D.(1)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :y=k (x+2
:y=k (x+2![]() )与圆O:
)与圆O:![]() 相交于A、B两点,O是坐标原点,
相交于A、B两点,O是坐标原点,![]() ABO的面积为S.
ABO的面积为S.
(1)试将S表示成的函数S(k),并求出它的定义域;
(2)求S的最大值,并求取得最大值时k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:A={x|2x2﹣3ax+a2<0},q:B={x|x2+3x﹣10≤0}.
(1)求A;
(2)当a<0时,若¬p是¬q的必要不充分条件,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设顶点在原点,焦点在![]() 轴上的拋物线过点
轴上的拋物线过点![]() ,过
,过![]() 作抛物线的动弦
作抛物线的动弦![]() ,
, ![]() ,并设它们的斜率分别为
,并设它们的斜率分别为![]() ,
, ![]() .
.
(Ⅰ)求拋物线的方程;
(Ⅱ)若![]() ,求证:直线
,求证:直线![]() 的斜率为定值,并求出其值;
的斜率为定值,并求出其值;
(III)若![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出其坐标.
恒过定点,并求出其坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲乙两个城市分别随机抽取16台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为![]() 中位数分别为
中位数分别为![]() 则( )
则( )

A. x甲<x乙,m甲>m乙 B. x甲>x乙,m甲>m乙
C. x甲>x乙,m甲<m乙 D. x甲<x乙,m甲<m乙
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某几何体的三视图都是直角三角形,则该几何体的体积等于__________.
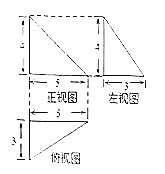
【答案】10
【解析】几何体为三棱锥,(高为4,底面为直角三角形),体积为![]()
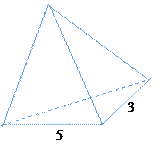
点睛:空间几何体体积问题的常见类型及解题策略
(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.
(2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.
(3)若以三视图的形式给出几何体,则应先根据三视图得到几何体的直观图,然后根据条件求解.
【题型】填空题
【结束】
15
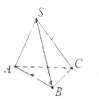
【题目】如图:在三棱锥![]() 中,已知底面
中,已知底面![]() 是以
是以![]() 为斜边的等腰直角三角形,且侧棱长
为斜边的等腰直角三角形,且侧棱长![]() ,则三棱锥
,则三棱锥![]() 的外接球的表面积等于__________.
的外接球的表面积等于__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在空间四边形ABCD中,点E,H分别是边AB,AD的中点,点F,G分别是边BC,CD上的点,且![]() ,则下列说法正确的是________.(填写所有正确说法的序号)
,则下列说法正确的是________.(填写所有正确说法的序号)

①EF与GH平行; ②EF与GH异面;
③EF与GH的交点M可能在直线AC上,也可能不在直线AC上;
④EF与GH的交点M一定在直线AC上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com