
【题目】如图,在边长为![]() 的菱形
的菱形![]() 中,
中,![]() .点
.点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,点
上,点![]() 与点
与点![]() ,
,![]() 不重合,
不重合,![]() ,
,![]() .沿
.沿![]() 将
将![]() 翻折到
翻折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)当![]() 与平面
与平面![]() 所成的角为
所成的角为![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知动直![]() :x+my-2m=0与动直线
:x+my-2m=0与动直线![]() :mx-y-4m+2=0相交于点M,记动点M的轨迹为曲线C.
:mx-y-4m+2=0相交于点M,记动点M的轨迹为曲线C.
(1)求曲线C的方程;
(2)过点P(-1,0)作曲线C的两条切线,切点分别为A,B,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)是奇函数,且满足f(3-x)=f(x),f(-1)=3,数列{an}满足a1=1且an=n(an+1-an)(n∈N*),则f(a36)+f(a37)=( )
A. ![]() B.
B. ![]() C. 2D. 3
C. 2D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=nan+n,数列{bn}的前n项和为Tn,求满足不等式![]() 的n的最小值.
的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() (
(![]() 为大于0的常数).现随机抽取6件合格产品,测得数据如下:
为大于0的常数).现随机抽取6件合格产品,测得数据如下:

对数据作了初步处理,相关统计位的值如下表:

(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现从抽取的6件合格产品中再任选3件,记
内时为优等品.现从抽取的6件合格产品中再任选3件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望.
的分布列和期望.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为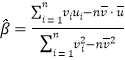 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有5道题,其中3道甲类题![]() ,2道乙类题
,2道乙类题![]() 。
。
(1)若从这5道题中任选2道,求这2道题至少有1道题是乙类题的概率;
(2)若从甲类题、乙类题中各选1道题,求这2道题包括![]() 但不包括
但不包括![]() 的概率。
的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com