
已知平面向量![]() ,
,![]()
(1)证明:![]() ;
;
(2)若存在实数![]() ,满足
,满足![]() ,
,![]() ,且
,且![]() ,试 求出
,试 求出![]() 关于
关于![]() 的关系式,即
的关系式,即![]() ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m ![]()
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源:山东省莒南一中2008-2009学年度高三第一学期学业水平阶段性测评数学理卷 题型:044
已知平面向量![]()
(1)证明:![]() ;
;
(2)若存在不同时为零的实数k和t,使![]() ,试求s=f(t)的函数关系式;
,试求s=f(t)的函数关系式;
(3)若s=f(t)在[1,+∞)上是增函数,试求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知平面向量![]() =(
=(![]() –1),
–1), ![]() =(
=(![]() ).
).
(1)证明![]() ⊥
⊥![]() ;
;
(2)若存在不同时为零的实数k和t,使![]() =
=![]() +(t2–3)
+(t2–3) ![]() ,
,![]() =–k
=–k![]() +t
+t![]() ,且
,且![]() ⊥
⊥![]() ,试求函数关系式k=f(t);
,试求函数关系式k=f(t);
(3)据(2)的结论,讨论关于t的方程f(t)–k=0的解的情况.
查看答案和解析>>
科目:高中数学 来源:2014届浙江省温州市高一第二学期期中考试数学试卷(解析版) 题型:解答题
已知平面向量 =(
=(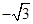 ,1),
,1),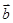 =(
=( ),
),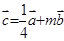 ,
, ,
, .
.
(1)当 时,求
时,求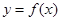 的取值范围;
的取值范围;
(2)设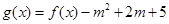 ,是否存在实数
,是否存在实数 ,使得
,使得 有最大值2,若存在,求出所有满足条件的
有最大值2,若存在,求出所有满足条件的 值,若不存在,说明理由
值,若不存在,说明理由
查看答案和解析>>
科目:高中数学 来源:2010年福建省八县(市高一下学期期末联考(文科)数学卷 题型:解答题
(本小题满分14分)
已知平面向量 =(
=( ,1),
,1), =(
=( ),
), ,
, ,
,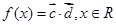 .(1)当
.(1)当 时,求
时,求 的取值范围;
的取值范围;
(2)设 ,是否存在实数
,是否存在实数 ,使得
,使得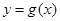 有最大值
有最大值 ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的 值,若不存在,说明理由.
值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com